(1) 嵗昗曄姺
(2) 儗儞僟儕儞僌
偑崅懍偵孞傝曉偝傟偰偄傞丅杮峞偱偼丄(1) 偺嵗昗曄姺偱巊傢傟偰偄傞傾僼傿儞曄姺偵偮偄偰愢柧偡傞丅
傑偢丄崅峑偺悢妛乮戙悢丒婔壗乯偱偼峴楍偱嵗昗曄姺傪峴偆師偺傛偆側堦師曄姺傪廗偭偨丅揰
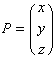 傪揰
傪揰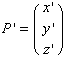 偵堏偡応崌丄曄姺峴楍
偵堏偡応崌丄曄姺峴楍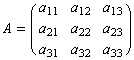 傪梡偄偰
傪梡偄偰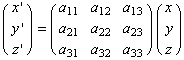 <=>
<=> 偲昞偝傟傞丅
偙偺峴楍A偼乽奼戝丒弅彫 (scaling)乿丄乽夞揮(rotation)乿偺崌惉偲側偭偰偄傞丅
側偤側傜偽丄
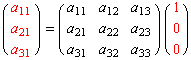
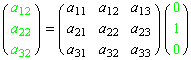
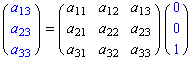
偲側傝丄奺婎掙
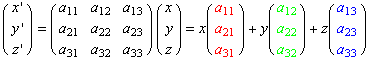
偲側傝丄婎掙
暯栰戱堦
嵟嬤偺僎乕儉婡乮僾儗僀僗僥乕僔儑儞丄僎乕儉僉儏乕僽丄X-Box 側偳乯偱偼僉儍儔僋僞乕偑懡妏宍偺廤崌乮億儕僑儞乯偱昞尰偝傟偰偄傞丅懡妏宍偼晛捠娙扨偺偨傔偵嶰妏宍偱昞尰偝傟傞丅僎乕儉偱僐儞僩儘乕儔傪憖嶌偟偰僉儍儔僋僞乕傪堏摦偝偣傞応崌傪峫偊傞偲丄傑偢億儕僑儞偺嵗昗傪寁嶼偟捈偡乮偙偺嶌嬈傪嵗昗曄姺偲尵偆乯丅偦偺屻丄偦偺嶰師尦偺嵗昗傪僥儗價偺僗僋儕乕儞偵崌偆傛偆偵擇師尦偺嵗昗偵曄姺偟偰乮搳塭偲尵偆丅偙傟傕屻偱愢柧偡傞傛偆偵嵗昗曄姺偺堦晹偲偟偰偲傜偊傞偙偲偑偱偒傞乯丄偦偺擇師尦偺嵗昗僨乕僞傪傕偲偵怓傪揾偭偨傝偟偰夋柺偵奊傪昤偔乮儗儞僟儕儞僌偲尵偆乯丅
偙偺傛偆側嶌嬈偑崅懍偱弖帪偵峴傢傟偰偄傞偨傔偵丄妸傜偐偵鉟楉側塮憸偑摦偄偰僎乕儉偑偱偒傞偺偱偁傞丅嵶偐偔尵偆偲丄晛捠1/60昩枅偵夋柺傪昤偒曄偊偰僷儔僷儔枱夋偺傛偆偵傾僯儊乕僔儑儞傪尒偣偰偄傞偺偱偁傞丅傾僯儊乕僔儑儞偺堦偮偺夋柺傪乽僼儗乕儉乿偲尵偄丄堦昩娫偵60夞夋柺傪昤偒曄偊傞応崌丄乽昩娫60僼儗乕儉乿偲尵偆丅僎乕儉婡偺怱憻晹偺僐儞僺儏乕僞偱偁傞CPU偼夋柺昤夋偺張棟偩偗傪峴偊偽椙偄偲偄偆栿偱偼側偔丄杮棃偺栚揑偱偁傞僎乕儉偺恑峴忬嫷偺張棟傪偡傞昁梫傕偁傝丄愄偺抶偄CPU偱偼夋柺傪昤偔張棟偑娫偵崌傢側偔側傞偙偲傕偁偭偨丅椺偊偽僼傽儈僐儞偺僌儔僨傿僂僗乮僐僫儈乯偱揋傗抏偑偄偭傁偄弌尰偟偨偲偒偵偼傕偺偡偛偔摦偒偑僗儘乕偵側傞応崌偑偁偭偨偑丄偦傟偼杮棃偺僎乕儉偺恑峴張棟乮抏偑摉偨偭偨偐偳偆偐側偳乯偑娫偵崌傢側偄偐傜夋柺偺峏怴傪椺偊偽1/60昩偐傜1/30昩偵堦帪揑偵棊偲偡傛偆側張棟傪偟偰偄傞偐傜偱偁傞乮偨偩偟丄僼傽儈僐儞偺帪戙偵偼億儕僑儞側偳巊傢偢丄僉儍儔僋僞乕傪扨偵僪僢僩偺廤崌偱昤偄偰偄偨偩偗偱偁傞乯丅僥儗價(CRT)偑夋柺傪峏怴偡傞僗僺乕僪偑寛傑偭偰偄傞偐傜乮揹巕廵傪僗僀乕僾偟偰偄傞偐傜乯丄彮偟僎乕儉帺懱偺張棟偑抶傟偨偐傜偲偄偭偰丄彮偟偩偗夋柺偺峏怴傪抶傜偣傞偲偄偆偙偲偑弌棃側偄偐傜偱偁傞丅偮傑傝丄張棟偑彮偟抶傟偨偲偟偰傕夋柺偺峏怴懍搙偼惍悢暘偺1偵偡傞偟偐側偄丅
幚嵺偵偼塮憸怣崋傪弌椡偡傞價僨僆僠僢僾偼夋柺偺墶曽岦偵揹巕傪憱嵏偟廔傢偭偨偙偲傪揱偊傞悈暯摨婜妱崬傒(HSYNC)偲廲曽岦偵堦夋柺暘揹巕傪憱嵏偟廔傢偭偨偙偲傪揱偊傞悅捈摨婜妱崬傒(VSYNC)傪CPU偵懳偟偰弌偟偰偍傝丄VSYNC妱崬傒偵崌傢偣偰夋柺傪昤偒曄偊傞傛偆偵偟偰偄傞(梋択偩偑丄HSYNC妱傝崬傒傪棙梡偟偰夋柺傪墶曽岦偵僌僯儍僌僯儍偲偆偹傜偣傞儔僗僞乕僗僋儘乕儖偲偄偆僥僋僯僢僋傕偁傞)丅嵟嬤偺僎乕儉婡偱偼嵗昗曄姺偲儗儞僟儕儞僌傪峴偆摿暿側愱梡僠僢僾偑偁偭偰丄CPU偼嵗昗偩偗偦偺夞楬偵搉偟偰屻偼帺暘偺巇帠偵愱擮偱偒傞傛偆偵側偭偰偄傞丅
梋択偱偁傞偑丄儗儞僟儕儞僌偺撪梕偵偮偄偰愢柧偡傞偲丄億儕僑儞偺擇師尦僨乕僞傪尦偵夋柺乮惓妋偵偼VRAM, 價僨僆RAM乯偵昤偄偰偄偔栿偩偑丄夋柺偐傜偼傒弌傞億儕僑儞偼昤偐側偄傛偆偵偟偨傝丄夋柺偺抂傪傑偨偖億儕僑儞偼夋柺撪偵巆傞晹暘偩偗傪昤夋偡傞丅偙偺嶌嬈傪僋儕僢僺儞僌(Clipping)偲尵偆丅墱偵偁傞億儕僑儞偑庤慜偺億儕僑儞偵塀傟傞傛偆側張棟傪偡傞偺偵傛偔Z僶僢僼傽朄偑梡偄傜傟傞丅偙傟傜偺嶌嬈傕尰嵼偱偼愱梡夞楬偑帺摦揑偵峴偆傛偆偵側偭偰偄傞丅
師偵怓晅偗偵偮偄偰愢柧偡傞丅億儕僑儞偺柺偺朄慄儀僋僩儖傪巊偭偰億儕僑儞撪傪摨堦怓偱揾傞偲丄僉儍儔僋僞乕偑僇僋僇僋偵尒偊偰偟傑偆乮僙僈僒僞乕儞偺僎乕儉偱傛偔尒傜傟偨乯丅偦偙偱丄億儕僑儞偵怓傪揾傞偲偒偵側傞傋偔妸傜偐偵尒偊傞傛偆偵岺晇偝傟偰偄傞丅傑偢丄僌儘乕僔僃乕僨傿儞僌偲屇偽傟傞曽朄偵偮偄偰愢柧偡傞丅嵟弶偵偁傞億儕僑儞偵偮偄偰椬愙偡傞億儕僑儞偺暯嬒偺朄慄儀僋僩儖傪巊偭偰捀揰偺埵抲偱偺朄慄儀僋僩儖傪媮傔丄偦偺朄慄儀僋僩儖傪巊偭偰怓傪寛傔傞丅師偵丄偦傟傜偺捀揰偺怓傪億儕僑儞偺柺撪偵撪憓偡傞偲尒堘偊傞傎偳妸傜偐偵尒偊傞偺偱偁傞丅僾儗僀僗僥乕僔儑儞偱偼僌儘乕僔僃乕僨傿儞僌偑僴乕僪僂僃傾偱梡堄偝傟偰偄偨丅側偍丄僙僈僒僞乕儞偱偼僌儘乕僔僃乕僨傿儞僌偑僴乕僪僂僃傾偱梡堄偝傟偰偄側偐偭偨偨傔丄僾儗僀僗僥乕僔儑儞偵偔傜傋偰僉儍儔僋僞乕偑僈僞僈僞偩偭偨偺偱偁傞丅傛傝崅搙側傕偺偱偼捀揰偺朄慄儀僋僩儖偺暯嬒抣傪柺撪偵撪憓偟偰僗儉乕僘偵怓偯偗偡傞僼僅乕儞僔僃乕僨傿儞僌偑偁傞丅
側偍丄朄慄儀僋僩儖偐傜偦偺揰偺怓傪寛傔傞曽朄偵傕丄扨弮偵岝慄偑偦偙偵摓棃偡傞妏搙偲偺撪愊傪庢傞曽朄偲丄暔懱枅偵岝偺媧廂棪傪掕媊偟偰丄岝偺暔懱偵傛傞懡廳斀幩傕峫椂偡傞曽朄側偳偑偁傞丅屻幰偺怓晅偗曽朄偼儗僀僩儗乕僔儞僌(Ray Tracing)偲尵傢傟丄乽僕儏儔僔僢僋僷乕僋乿丄乽傾億儘13乿側偳偺塮夋偱傕巊傢傟偰偄傞曽朄偱丄嬃偔掱儕傾儖側塮憸傪嶌傝弌偡丅巆擮側偑傜丄儕傾儖僞僀儉張棟偑梫媮偝傟傞僎乕儉婡偱偼傑偩儗僀僩儗乕僔儞僌偑巊傢傟偰偄側偄偑丄彨棃幚梡壔偝傟偰偄偔偙偲偼娫堘偄側偄丅傑偨丄儗僀僩儗乕僔儞僌傛傝傕傛傝儕傾儖側塮憸傪嶌傝弌偡曽朄傕偄偔偮偐偁傞偑丄傛傝懡偔偺寁嶼帪娫偑偐偐傞偨傔丄尰嵼偱偼塮夋惢嶌側偳偵儗僀僩儗乕僔儞僌偑懡偔巊傢傟偰偄傞丅
偝偰丄慜抲偒偑挿偔側偭偨偑僎乕儉偱夋柺傪昤偔嶌嬈傪傑偲傔傞偲
(1) 嵗昗曄姺
(2) 儗儞僟儕儞僌
偑崅懍偵孞傝曉偝傟偰偄傞丅杮峞偱偼丄(1) 偺嵗昗曄姺偱巊傢傟偰偄傞傾僼傿儞曄姺偵偮偄偰愢柧偡傞丅
傑偢丄崅峑偺悢妛乮戙悢丒婔壗乯偱偼峴楍偱嵗昗曄姺傪峴偆師偺傛偆側堦師曄姺傪廗偭偨丅揰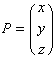 傪揰
傪揰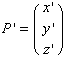 偵堏偡応崌丄曄姺峴楍
偵堏偡応崌丄曄姺峴楍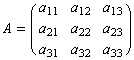 傪梡偄偰
傪梡偄偰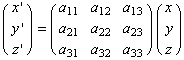 <=>
<=> ![]() (1)
(1)
偲昞偝傟傞丅
偙偺峴楍A偼乽奼戝丒弅彫 (scaling)乿丄乽夞揮(rotation)乿偺崌惉偲側偭偰偄傞丅
側偤側傜偽丄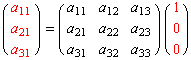
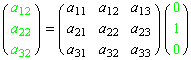
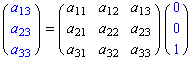
偲側傝丄奺婎掙![]() ,
,![]() ,
,![]() 偼
偼![]() ,
,![]() ,
,![]() 偵偦傟偧傟曄姺偝傟傞丅暿偺尵偄曽傪偡傞偲丄
偵偦傟偧傟曄姺偝傟傞丅暿偺尵偄曽傪偡傞偲丄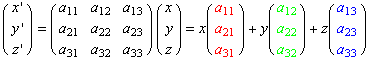
偲側傝丄婎掙![]() ,
,![]() ,
,![]() 偱挘傜傟傞嬻娫偼婎掙
偱挘傜傟傞嬻娫偼婎掙![]() ,
,![]() ,
,![]() 偱挘傜傟傞嬻娫偵堏傝丄壓偺恾偺僀儊乕僕偺傛偆偵側傞丅
偱挘傜傟傞嬻娫偵堏傝丄壓偺恾偺僀儊乕僕偺傛偆偵側傞丅
![[Graphics:HTMLFiles/index_22.gif]](HTMLFiles/index_22.gif)
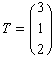 偺暯峴堏摦偼峴楍偱昞偡偙偲偑偱偒偢丄
偺暯峴堏摦偼峴楍偱昞偡偙偲偑偱偒偢丄暯峴堏摦傕峴楍偱埖偄丄峴楍偺愊偺寢崌婯懃乮![]() , 墘嶼偺弴斣傪曄峏偱偒傞惈幙乯偑揔梡偱偒傞傛偆偵偡傞偨傔偵師尦傪侾偮憹傗偡丅峴楍偺寢崌婯懃偑巊偊傞偲偄偆偙偲偼寁嶼検傪尭傜偟丄墘嶼傪崅懍壔偡傞偨傔偵旕忢偵廳梫偱偁傞丅
, 墘嶼偺弴斣傪曄峏偱偒傞惈幙乯偑揔梡偱偒傞傛偆偵偡傞偨傔偵師尦傪侾偮憹傗偡丅峴楍偺寢崌婯懃偑巊偊傞偲偄偆偙偲偼寁嶼検傪尭傜偟丄墘嶼傪崅懍壔偡傞偨傔偵旕忢偵廳梫偱偁傞丅
峴楍偺寢崌婯懃偺廳梫惈傪愢柧偡傞偨傔偵丄億儕僑儞偺捀揰傪![]() 乮儀僋僩儖乯偲偟丄偦傟傪嵗昗曄姺乮儀僋僩儖偵懳偡傞峴楍偺妡偗嶼偱昞尰偝傟傞乯偡傞偙偲傪峫偊傞丅椺偊偽丄傑偢尨揰偵懳偟偰x幉夞傝偺夞揮(
乮儀僋僩儖乯偲偟丄偦傟傪嵗昗曄姺乮儀僋僩儖偵懳偡傞峴楍偺妡偗嶼偱昞尰偝傟傞乯偡傞偙偲傪峫偊傞丅椺偊偽丄傑偢尨揰偵懳偟偰x幉夞傝偺夞揮(![]() )傪偟偰丄尨揰偵懳偟偰奼戝偡傞(
)傪偟偰丄尨揰偵懳偟偰奼戝偡傞(![]() )偙偲傪峫偊傞丅捀揰
)偙偲傪峫偊傞丅捀揰![]() 傪偙偺傛偆偵嵗昗曄姺偟偰
傪偙偺傛偆偵嵗昗曄姺偟偰![]() 偵堏偭偨偲偡傞偲丄
偵堏偭偨偲偡傞偲丄![]()
偲彂偗傞丅忋偺塃曈偺寁嶼偼峴楍偺寢崌婯懃傛傝丄![]()
偲彂偔偙偲傕偱偒傞丅偙偺傛偆偵丄峴楍偺寢崌婯懃傪巊偆偲愭偵曄姺峴楍偩偗傪寁嶼偟偰堦偮偵傑偲傔偰偍偄偰丄屻偱摨偠峴楍傪慡捀揰偵偐偗傞偩偗偱椙偄偙偲偵側傝丄寁嶼検傪尭傜偟偰崅懍壔偡傞偙偲偑偱偒傞忋偵幃偑鉟楉偱尒捠偟偑椙偄丅
偟偐偟丄巆擮側偑傜幃(1)偱掕媊偝傟傞堦師曄姺偱偼暯峴堏摦傪捀揰傊偺峴楍偺妡偗嶼偱昞尰偡傞偙偲偑偱偒側偄丅偦偙偱丄師偺傛偆偵嵗昗偺嵟屻偵1傪擖傟偨僟儈乕嵗昗傪峫偊偨峴楍傪峫偊傞丅曄姺屻偵嵗昗傪撉傒偲傞偲偒偼嵍曈儀僋僩儖嵟屻偺"1"偺僟儈乕嵗昗傪柍帇偡傞丅 (3)
(3)
偙偺傛偆偵掕媊偡傞偲丄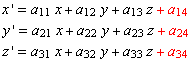
偲側傝丄暯峴堏摦傕峴楍偺妡偗嶼偱昞尰弌棃偰偄傞丅幃(3)偺曄姺傪傾僼傿儞曄姺乮堦斒偵偼慄宍曄姺偲暯峴堏摦偺崌惉傪昞偟丄係師尦偺峴楍昞尰傪昞偡栿偱偼側偄乯偲尵偆丅
傑偨丄屻弎偡傞偑幃(3)偱偮偄偱偵搳塭張棟傪偡傞偙偲傕偱偒傞丅摟帇搳塭曄姺傪偡傞傛偆偵奼挘偟偨応崌偼丄 (4)
(4)
偲偟偰丄嵟屻偵![]() 傪
傪![]() 偱妱偭偰偍偔丅徻偟偔偼摟帇搳塭曄姺偺愡偱弎傋傞丅
偱妱偭偰偍偔丅徻偟偔偼摟帇搳塭曄姺偺愡偱弎傋傞丅
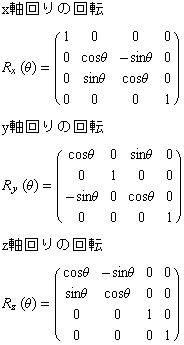
暯峴堏摦偲偙傟傜偺夞揮傪慻傒崌傢偣傟偽擟堄偺揰偺夞傝偺夞揮偑壜擻偱偁傞丅幚嵺偵偼暯峴堏摦偲俀偮偺堎側傞幉偺夞傝偺夞揮偩偗偱擟堄偺夞揮偑壜擻偱偁傞丅
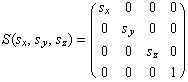
尨揰傪拞怱偲偟偰x,y,z幉曽岦偵偦傟偧傟![]() 偩偗怢弅偡傞丅偙傟傕暯峴堏摦偲慻傒崌傢偣傞偲擟堄偺揰傪拞怱偲偡傞奼戝丒弅彫偑壜擻偱偁傞丅
偩偗怢弅偡傞丅偙傟傕暯峴堏摦偲慻傒崌傢偣傞偲擟堄偺揰傪拞怱偲偡傞奼戝丒弅彫偑壜擻偱偁傞丅
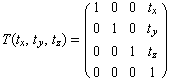
幃(3)偺傾僼傿儞曄姺傪巊偆偲丄搳塭曄姺傕摨帪偵弌棃傞傛偆偵側傞丅![]() 傪岝偺廂懇揰偲偟丄
傪岝偺廂懇揰偲偟丄![]() 傪暔懱忋偺捀揰偲偡傞偲丄
傪暔懱忋偺捀揰偲偡傞偲丄![]() 傪寢傇捈慄忋偺揰
傪寢傇捈慄忋偺揰![]() 偼
偼![]() 傪僷儔儊乕僞偲偟偰師偺曽掱幃傪枮偨偡丅乮捈慄偺曽掱幃乯
傪僷儔儊乕僞偲偟偰師偺曽掱幃傪枮偨偡丅乮捈慄偺曽掱幃乯![]()
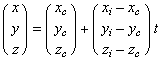
![]() (
(![]() plane)偵搳塭偡傞偲丄
plane)偵搳塭偡傞偲丄![]()
![]()
![]()
傛偭偰丄![]() 傪
傪![]() 偵曄姺偡傞摟帇搳塭曄姺峴楍偼師偺傛偆偵側傞丅
偵曄姺偡傞摟帇搳塭曄姺峴楍偼師偺傛偆偵側傞丅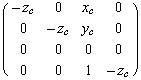 (5)
(5)
![[Graphics:HTMLFiles/index_58.gif]](HTMLFiles/index_58.gif)
嵗昗曄姺偟偨屻幃(5)偺峴楍傪妡偗丄幃(4)偺![]() 偱
偱![]() 傪妱偭偰偍偗偽摟帇搳塭偟偨嵗昗偵側傞丅
傪妱偭偰偍偗偽摟帇搳塭偟偨嵗昗偵側傞丅
In[1]:=

![[Graphics:HTMLFiles/index_62.gif]](HTMLFiles/index_62.gif)
![[Graphics:HTMLFiles/index_63.gif]](HTMLFiles/index_63.gif)
In[2]:=
![Module[{w, p2}, (* 曄姺峴楍偺掕媊 *) P[xc_, yc_, zc_] := (-zc 0 xc 0 ) ; (* ... 0 0 0 0 0 0 1 -zc](HTMLFiles/index_64.gif)
![[Graphics:HTMLFiles/index_65.gif]](HTMLFiles/index_65.gif)
![[Graphics:HTMLFiles/index_66.gif]](HTMLFiles/index_66.gif)
Out[2]=
![]()
[嶲峫暥專]
S.僴儕儞僩儞:乽僐儞僺儏乕僞 僌儔僼傿僢僋僗[I]乿, 儅僌儘僂僸儖僽僢僋, 徍榓63擭
S.僴儕儞僩儞:乽僐儞僺儏乕僞 僌儔僼傿僢僋僗[II]乿, 儅僌儘僂僸儖僽僢僋, 徍榓63擭
Converted by Mathematica (October 4, 2003)