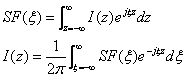フーリエ変換法 (Fourier Transform Method)

― 連続波源分布 ―

2002 東京工業大学 平野拓一

1. 波源分布と遠方界指向性のフーリエ変換の関係

電磁界の遠方界は次のように表される。

(1)

(2)

(3)

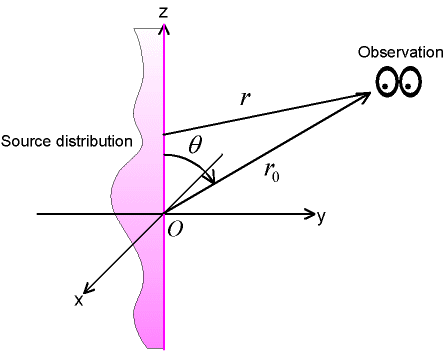
図 1 z 軸上線波源分布

ここで、観測点が無限に遠く離れているとき次の近似が成り立つ。

ここで、とおくと、 (4)

(5)

指向性は上の式で距離によらずに角度だけの項で決まるから、

というスペースファクタ(Space Factor)を定義する。

は のフーリエ変換になっている。つまり、次のフーリエ変換対が成り立つ。

(6)

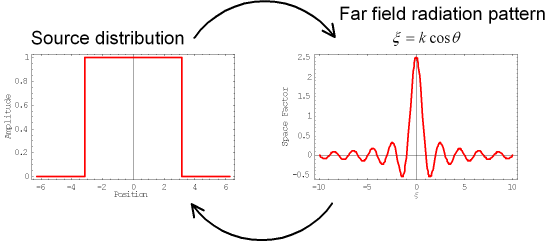
図 2 波源分布と遠方界のフーリエ変換の関係

ここで、遠方界指向性は式(2)、式(5)より に比例する。ここで、式(4)の変換を考えると、 は式(4)の媒介変数表示を介して合成関数としてと指向性を意味している。は波源分布と指向性を結びつける数式表現を簡単にするために導入された変数変換である。

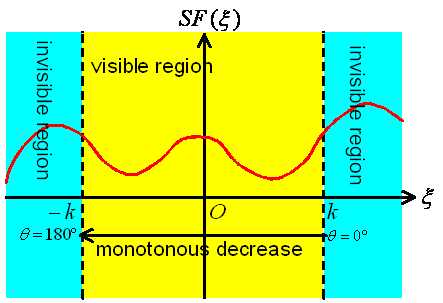
図 3 スペースファクタ

式(4)よりはのときとなり、+1から-1までの値しかとらないので、となってはからまで値を取り、によって範囲を制限される。また、のによる変化は線形ではないが、はからまで単調減少するのではがからまでの値で物理的指向性に対応すると考えればよい。の物理的に指向性を意味するの範囲を可視域(visible region)と言い、それ以外の範囲を不可視域(invisible region)と言う。

そのような意味で、は単にスペースファクタの範囲を限定するパラメータと考えればよく、実際に指向性合成をするときにはスペースファクタをの関数と見ると数式的に複雑になるので、が直接に対応すると考えて指向性を設計する。

2. フーリエ変換法

フーリエ変換法は所望の指向性を作り出す波源分布を計算する方法である。1章の話がわかっていれば話は簡単である。式(6)の下の式の逆フーリエ変換を用いて簡単に波源分布を求めることができる。ただし、その場合連続波源で無限長になってしまうが、十分長いアレーを使うとすれば良い近似を与える。