シェルクノフの多項式法 (Schelkunoff Polynomial Method)

平野拓一

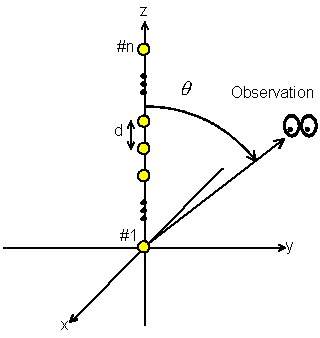
図 1 等間隔リニアアレー

図 1のアレーファクタは次のようになる。

(1)

ここで、

(2)

とおくと

(3)

代数学の基本定理から、式(3)の多項式は次のように因数分解できる。

(4)

ここで、はの根であり、となる点だからそれらのに対応する

は指向性のヌルとなる。

ヌルの角度を指定した指向性を作りたいとき、式(4)を先に作り、の多項式の係数を式(3)と比較して素子重みを決定する方法がシェルクノフの多項式法(Schelkunoff Polynomial Method)である。ただし、ヌルが指定した角度にくることは確実だが、全体のビームの形がどうなるかは定かではない。

（例）

θ=θ1,θ2方向にヌルを向ける波長間隔アレーを作りたいとき

とし、

(5)

とする。また、アレーファクタは素子重み係数を使って表現すると

と書けるので、

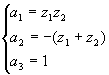
となる。つまり３素子アレーである。また式(5)で重解を持つように設定すれば３素子以上ならば任意の素子数で実現できる。３素子以下では２つの方向にヌルを向けることは不可能である。