ウッドワード・ローソン法 (Woodward-Lawson Method)

― 連続波源分布 ―

平野拓一

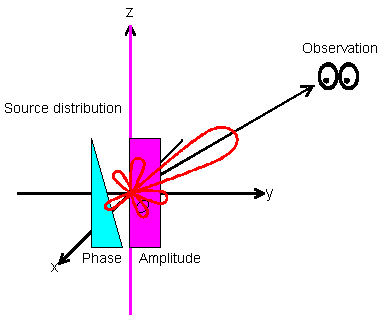
図 1 z 軸上線波源分布

フーリエ変換法のところで「波源分布と遠方界指向性はフーリエ変換の関係にある」ことを説明した。図 1のように波源分布がパルス関数形のとき、遠方界指向性は sinc 関数となる。その波源分布の振幅は一定のまま、位相に傾きをつけるとメインビーム方向が傾く。このメインビーム方向を傾けた sinc 関数をいくつか重ね合わせて所望の指向性を得る方法がウッドワード・ローソン法 (Woodward-Lawson Method) である。

本手法はレーダーアンテナによく用いられるコセカント２乗パターンを作るのにも使われている。

設計手順

Step. 1

設計したい指向性を決める。ここでは例として、つぎのようなからの間だけにビームを作るセクトラルビームを合成する。

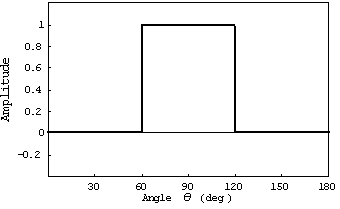
Step. 2

サンプリング点を決める。サンプリング点は自由には決められず、波源長の関数となる。

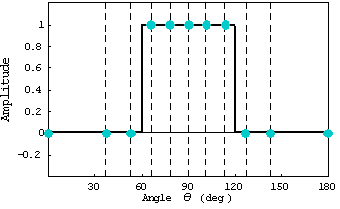
Step. 3

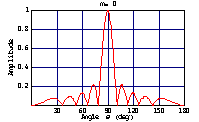
次のような振幅が一定で、位相が直線的に変化する基底関数を波源上に仮定する。それらの波源による遠方界指向性は sinc 関数形となる。それを重ね合わせて所望の指向性を近似するので、この波源基底関数を生成関数 (composing function)と呼ぶ。

→

→

→

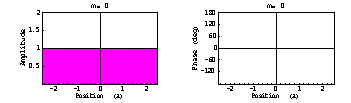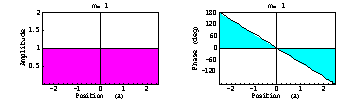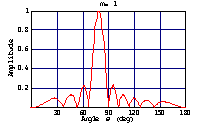
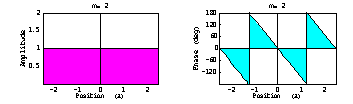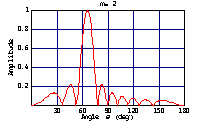
指向性を sinc 関数指向性の重ね合わせで表す。各サンプリング点では他の sinc 関数からの影響が無くなる。そのようにサンプリング点を選ぶ必要があったので、step2では自由にサンプリング点が選べなかったのである。

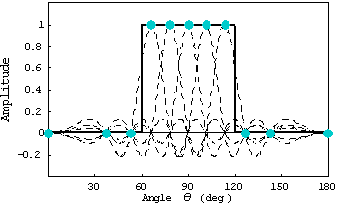
この波源長では次の赤い線のような指向性となる。波源長を長くすれば黒いセクトラルビームをより良く近似できるようになる。

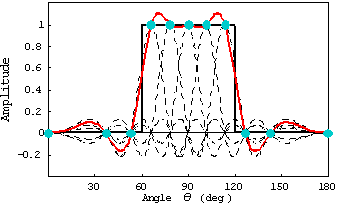
Step. 4

波源分布は一様分布で位相が直線的に変化する分布（それが上の sinc 関数指向性を作り出している）の重ね合わせで表現できる。

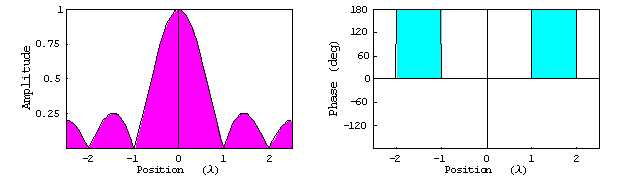
このようにして設計が完了する。

アレーアンテナにしたいときは設計された連続波源の中に十分狭い間隔(1/2波長以下)で素子を配置し、連続波源の重みを与えればよい。