Circularly Polarized Wave by Two
Linearly Polarized Waves
2003/01/06 Takuichi Hirano (Tokyo Institute of
Technology)

Fig. 1 Coordinates
The condition that the sum of two linearly polarized
waves ![]() , traveling toward
, traveling toward ![]() direction as
shown in Fig. 1, becomes circularly polarized wave is proved here,
where
direction as
shown in Fig. 1, becomes circularly polarized wave is proved here,
where ![]() is the
wavenumber.
is the
wavenumber.
The coordinates are shown in Fig. 1. In ![]() coordinates,
coordinates, ![]() and
and ![]() axes are crossing
with angle
axes are crossing
with angle ![]() and
and ![]() and
and ![]() axes coincide
with
axes coincide
with ![]() and
and ![]() axes,
respectively.
axes,
respectively. ![]() ,
,![]() ,
,![]() and
and ![]() indicate unit
vectors of
indicate unit
vectors of ![]() ,
,![]() ,
,![]() and
and ![]() axes,
respectively.
axes,
respectively. ![]() and
and ![]() are expressed by
are expressed by ![]() and
and ![]() as follows.
as follows.
![]() (1)
(1)
Consider the sum
of two linearly polarized waves whose axes of polarization are ![]() and
and ![]() , respectively, as shown in Fig. 1.
, respectively, as shown in Fig. 1.
![]() (2)
(2)
where ![]() and
and ![]() are complex
numbers (Phasor representation) as follows
are complex
numbers (Phasor representation) as follows
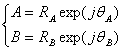 (3)
(3)
where ![]() ,
,![]() ,
,![]() and
and ![]() are real numbers.
are real numbers.
By substituting
Eq.(3) into Eq.(2) and using Eq.(1)
![]()
The circular
polarization condition in ![]() plane is applied
here.
plane is applied
here.
![]()
where + sign (upper)
in right hand side means the right hand circularly polarized wave (RHCP) while –
sign (lower) means the left hand one (LHCP) when the wave propagates toward +z
direction.
![]()
![]()
![]()
![]()
![]()
By Eq.(4)
![]() (6)
(6)
Substituting this
equation into Eq. (5) yields
![]()
![]()
![]()
![]()
![]()
![]()
![]()
where ![]() is an arbitrary
integer number.
is an arbitrary
integer number.
![]()
![]()
![]()
![]()
By substituting
this into Eq.(6)
![]()
The following two
conditions are obtained for circular polarization
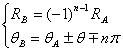
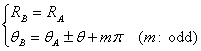
where + sign
(upper) in right hand side means the right hand circularly polarized wave
(RHCP) while – sign (lower) means the left hand one (LHCP) when the wave
propagates toward +z direction.