Electric Lines of Force of Infinitesimal Dipole
微小ダイポールから放射される電磁界の電気力線
By Takuichi Hirano (Tokyo Institute of Technology)
In[3]:=
![]()
![]()
Infinitesimal Dipole
微小ダイポール
In[5]:=
![]()
![]()
![]()
![]()
![]()
![]()
Prepare Animation
アニメーションの準備
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![((1 - 1/R^2) Sin[T - R] + Cos[T - R]/R)/(Cos[T - R] + Sin[T - R]/R) dR = 2 Cos[θ]/Sin[θ] dθ (Variables separable)](HTMLFiles/index_20.gif)
![Then, integrate this equation . <br /> -Log[Cos[T - R] + Sin[T - R]/R] = 2 Log[ Sin[θ] ] + C '](HTMLFiles/index_21.gif)
![Finnary, <br />[Cos[R - T] + Sin[R - T]/R] (Sin[θ])^2 = const .](HTMLFiles/index_22.gif)
Animation of Electric Lines of Force
(ContourPlot)
In[10]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
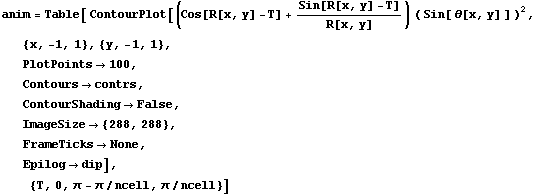
![[Graphics:HTMLFiles/index_31.gif]](HTMLFiles/index_31.gif)
![[Graphics:HTMLFiles/index_32.gif]](HTMLFiles/index_32.gif)
![[Graphics:HTMLFiles/index_33.gif]](HTMLFiles/index_33.gif)
![[Graphics:HTMLFiles/index_34.gif]](HTMLFiles/index_34.gif)
![[Graphics:HTMLFiles/index_35.gif]](HTMLFiles/index_35.gif)
![[Graphics:HTMLFiles/index_36.gif]](HTMLFiles/index_36.gif)
![[Graphics:HTMLFiles/index_37.gif]](HTMLFiles/index_37.gif)
![[Graphics:HTMLFiles/index_38.gif]](HTMLFiles/index_38.gif)
Out[17]=
| Created by Mathematica (January 24, 2006) |