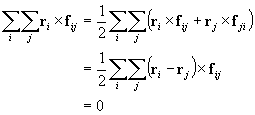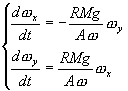歳差運動について
2002年1月11日 平野拓一
 1. 角運動量保存則
1. 角運動量保存則
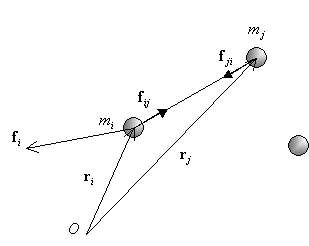
質量![]() の剛体が受ける外力を
の剛体が受ける外力を![]() , それが質量
, それが質量![]() の剛体と引き合う力を
の剛体と引き合う力を![]() とすると、
とすると、
ニュートンの運動方程式
![]()
![]()
![]()
ここで、
![]() (万有引力の法則、作用・反作用の法則)
(万有引力の法則、作用・反作用の法則)
より、最終項は
なぜならば![]() と
と![]() の方向は同じだからである。つまり、質点間の引力の効果が消える。
の方向は同じだからである。つまり、質点間の引力の効果が消える。
また、
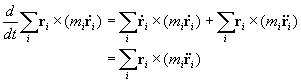
より左辺を変形すると、
![]()
ここで、
![]() (角運動量)
(角運動量)
![]() (原点を中心とする外力のモーメント、トルクとも言う)
(原点を中心とする外力のモーメント、トルクとも言う)
と定義すると
(例1) ケプラーの法則(面積速度一定)の法則の説明
式(1)より、太陽と地球が引き合う力は![]() に影響を与えないので、式(2)より、
に影響を与えないので、式(2)より、
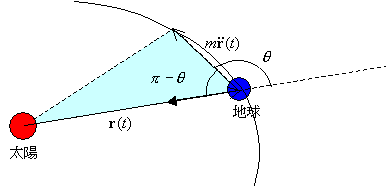
![]()
![]()
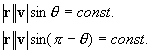
← 面積速度一定そのもの
2. 軸対称回転剛体の角運動量ベクトル
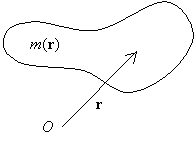
回転剛体の角運動量ベクトル
![]() (3)
(3)
2.1 軸対称で対称軸と回転軸が一致する場合
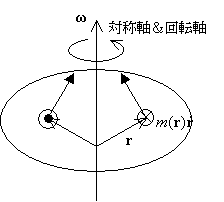
対称軸上にモーメントの基準を置いた場合、
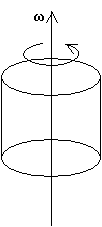
積分すると角運動量ベクトルの対称回転軸に垂直
な面内の成分は右図のように打ち消され、
対称回転軸方向の成分しか持たない。
回転体の回転方向に右ねじを回したときに
右ねぎが進む方向を持ち、大きさがその角速度![]()
である角速度ベクトル![]() を定義すると、
を定義すると、
回転体の角運動量は次のように書ける。
ただし、![]() は剛体の形、質量分布などで決まる
は剛体の形、質量分布などで決まる
定数である。
(例1) 人工衛星はなぜ自転させるか?
人工衛星は姿勢を保つために回転(自転)させている。
なぜ自転させると姿勢を保てるかは式(2), 式(4)を見ればわかる。
軸対称回転体は式(4)のような角運動量ベクトルを持つ。その角運動量ベクトルを変化させようとすると式(4)を式(2)に代入して
![]()
となる。元々あった角運動量ベクトルが大きい程、それを変化させようとする外力のモーメント![]() の効果は小さくなる。よって、高速で回転させたり
の効果は小さくなる。よって、高速で回転させたり![]() を大きくするとその回転軸
を大きくするとその回転軸![]() をなかなか変化させないような効果がある。これは「慣性の法則」そのものである。
をなかなか変化させないような効果がある。これは「慣性の法則」そのものである。
人工衛星も太陽風などのちょっとした影響で中心軸が回転して姿勢を崩さないように中心軸の周りに自転させてある。人工衛星は宇宙空間に浮いており、どこにも固定されてないので、モーメントは重心を中心としたものを考えるとよい。
また、人工衛星全体に一様な力がかかったときは外力によるモーメントは
![]()
と計算されて、軸対称対だから対称軸に関して
対称な点で打ち消されて角運動量は何ら変化しない。
(例2) ジャイロ
今では飛行機の位置情報は人工衛星から飛んでくる電波の時間差を利用したGPS(Global Positioning System)が使われるようになった(と思う)が、飛行機で位置や方位の情報をつかむためにはジャイロが使われていた(る?)。
ジャイロは軸対称高速回転体はその回転軸を変えにくいという性質を利用して方向をつかむものである。飛行機が飛び立つ前にジャイロを回転させ、そのときの方向を記録しておけば、空に飛び立った後もジャイロの回転軸と飛行機の進行方向がなす角を読み取ることによって、絶対的な方向が把握できる。
また、ジャイロはロボット姿勢検出センサーなどとしても使われている。
3. 歳差運動
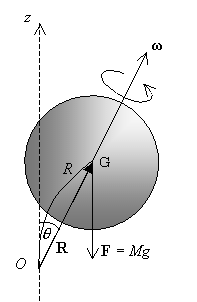
2章の結果より、右の図のように軸周りに
角速度![]() で回転する回転体が
で回転する回転体が![]() に固定されて
に固定されて
いるとする。![]() を中心とする角運動量
を中心とする角運動量![]() は、
は、
回転軸方向の向きを持ち、大きさが![]() の
の
角速度ベクトル![]() の方向と一致し、
の方向と一致し、
次のように書ける。
![]()
ただし、![]() は剛体の形、質量分布などで決まる
は剛体の形、質量分布などで決まる
定数である。
今、剛体として「こま」を考え、こまの下が![]()
だとする。こまの重心を![]() とし、全体の質量を
とし、全体の質量を![]()
とすると、
![]()
なる力が![]() にかかる。ただし、
にかかる。ただし、![]() は重力定数である。
は重力定数である。
すると、
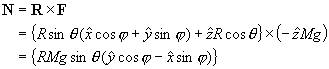
![]()
角運動量保存則より
![]()
つまり、角速度ベクトル![]() の向きは
の向きは![]() の向き(紙面の垂直奥方向)に変化していく。
の向き(紙面の垂直奥方向)に変化していく。![]() は常に
は常に![]() と鉛直方向の軸を含む面に垂直な方向となるので、
と鉛直方向の軸を含む面に垂直な方向となるので、![]() の鉛直成分と
の鉛直成分と![]() は一定となり、鉛直軸との角度
は一定となり、鉛直軸との角度![]() を保ちながら
を保ちながら![]() を通る鉛直軸の周りを円錐を描いて回転することになる。式を解いて説明すると次のようになる。
を通る鉛直軸の周りを円錐を描いて回転することになる。式を解いて説明すると次のようになる。
![]() は一定の説明
は一定の説明
![]()
ここで、式(2)の角運動量保存則を使うと
![]()
となる。![]() ならば、
ならば、
![]()
となる。
歳差運動の説明
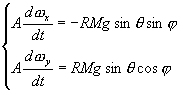
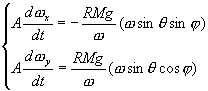
式(5)の上の式を時間微分すると
![]()
この式の右辺に式(5)の下の式を使うと
![]()
![]()
![]() (定数係数線形微分方程式を解く問題)
(定数係数線形微分方程式を解く問題)
![]()
また、式(5)の上の式から
![]()
![]() は時間に依らない任意定数で、初期条件によって定まる。
は時間に依らない任意定数で、初期条件によって定まる。
このように角速度
![]()
で鉛直方向軸(外力ベクトルの軸)の周りを回ることがわかる。これを「歳差運動(才差運動、さいさうんどう, precession)」と言う。
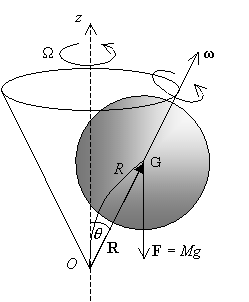
ここで、歳差運動の特徴を説明すると、鉛直軸と回転角のなす角![]() は一定であり、歳差運動の角速度
は一定であり、歳差運動の角速度![]() は
は![]() に依存しない。
に依存しない。
(例1) こま
こまを回すと軸がゆっくり回るが、それは歳差運動そのものである。
(例2) 地軸の歳差運動
地球の自転軸である地軸も太陽からの引力という外力のモーメントを受けて歳差運動を行っている。