
解説ドキュメントはこれから作ります。

以下のグラフにはCを基準音としたときのグラフを示します。 横軸は2和音を鳴らしたときのC以外のもう一つの音(音程に対応)です。 縦軸はそれぞれのグラフで異なります。
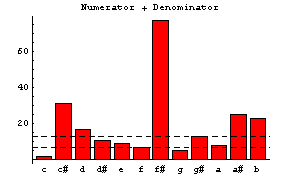
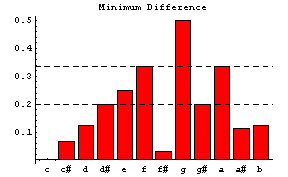
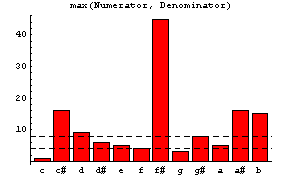
このグラフの描き方は 「平均律と純正律の和音の比較および協和音・不協和音の考察」 を参照してください。 全てのグラフに相関があります。 でも、これらのグラフで図2の基準が協和音・不協和音の判断基準として 物理的意味が一番明確だと思います。 つまり、倍音の周波数が互いに接近するほどうなりが生じます。 しかもうなりが生じる倍音もあればそうでない倍音もあって音が崩れたように感じます。 したがって、2つの音がよくとけ合うためにはそれらの倍音の周波数差は なるべく離れているほうが望ましいという結論になります。 こう思って不協和音を聞いてみると「和音の濁りというのは倍音のうなりだ」 と感じることができると思います(下のMIDIファイルで不協和音を聴いてください)。 正に上の図2は協和音・不協和音の判断基準として 定量的な指標を与えていると思われます(もちろん、倍音の含み方は音色によっても 違うので、同じ不協和音と言っても音色によってその度合いが異なると思われます)。 音楽では協和音(完全協和音、不完全協和音)と不協和音に分けていますが、 工学(Engineering)的にはそれらを明確に区別するのではなく、 協和音度として図2のグラフを用いるなどするのがより定量的でよい のではないでしょうか(明確に分けることができないことは楽典にも書かれていますが)。
| 度 | 音程名 | (全音数, 半音数) |
半音数 | 純正律 周波数比 |
協和音・ 不協和音 |
音 |  SMF File (MIDI) SMF File (MIDI) |
 MML MML |
|---|---|---|---|---|---|---|---|---|
| 1度 | 完全1度 | (0,0) | 0 | 1:1 | 完全協和音 | C, C | c_c_just.mid | c_c_just.mml |
| 2度 | 短2度 | (0,1) | 1 | 15:16 | 不協和音 | C, C# | c_c+_just.mid | c_c+_just.mml |
| 長2度 | (1,0) | 2 | 8:9 | 不協和音 | C, D | c_d_just.mid | c_d_just.mml | |
| 3度 | 短3度 | (1,1) | 3 | 5:6 | 不完全協和音 | C, D# | c_d+_just.mid | c_d+_just.mml |
| 長3度 | (2,0) | 4 | 4:5 | 不完全協和音 | C, E | c_e_just.mid | c_e_just.mml | |
| 4度 | 完全4度 | (2,1) | 5 | 3:4 | 完全協和音 | C, F | c_f_just.mid | c_f_just.mml |
| 増4度 | (3,0) | 6 | ? | 不協和音 | F, B | f_b_just.mid | f_b_just.mml | |
| 5度 | 減5度 | (2,2) | 6 | 32:45 | 不協和音 | C, F# | c_f+_just.mid | c_f+_just.mml |
| 完全5度 | (3,1) | 7 | 2:3 | 完全協和音 | C, G | c_g_just.mid | c_g_just.mml | |
| 6度 | 短6度 | (3,2) | 8 | 5:8 | 不完全協和音 | C, G# | c_g+_just.mid | c_g+_just.mml |
| 長6度 | (4,1) | 9 | 3:5 | 不完全協和音 | C, A | c_a_just.mid | c_a_just.mml | |
| 7度 | 短7度 | (4,2) | 10 | 9:16 | 不協和音 | C, A# | c_a+_just.mid | c_a+_just.mml |
| 長7度 | (5,1) | 11 | 8:15 | 不協和音 | C, B | c_b_just.mid | c_b_just.mml | |
| 8度 | 完全8度 | (5,2) | 12 | 1:2 | 完全協和音 | C, C | c_c2_just.mid | c_c2_just.mml |
やはり周波数比というのは純正律のものであり、それから少しずれているために 長3度の和音はかなりうなっている。
| 度 | 音程名 | (全音数, 半音数) |
半音数 | 純正律 周波数比 |
協和音・ 不協和音 |
音 |  SMF File (MIDI) SMF File (MIDI) |
 MML MML |
|---|---|---|---|---|---|---|---|---|
| 1度 | 完全1度 | (0,0) | 0 | 1:1 | 完全協和音 | C, C | c_c_temp.mid | c_c_temp.mml |
| 2度 | 短2度 | (0,1) | 1 | 15:16 | 不協和音 | C, C# | c_c+_temp.mid | c_c+_temp.mml |
| 長2度 | (1,0) | 2 | 8:9 | 不協和音 | C, D | c_d_temp.mid | c_d_temp.mml | |
| 3度 | 短3度 | (1,1) | 3 | 5:6 | 不完全協和音 | C, D# | c_d+_temp.mid | c_d+_temp.mml |
| 長3度 | (2,0) | 4 | 4:5 | 不完全協和音 | C, E | c_e_temp.mid | c_e_temp.mml | |
| 4度 | 完全4度 | (2,1) | 5 | 3:4 | 完全協和音 | C, F | c_f_temp.mid | c_f_temp.mml |
| 増4度 | (3,0) | 6 | ? | 不協和音 | F, B | f_b_temp.mid | f_b_temp.mml | |
| 5度 | 減5度 | (2,2) | 6 | 32:45 | 不協和音 | C, F# | c_f+_temp.mid | c_f+_temp.mml |
| 完全5度 | (3,1) | 7 | 2:3 | 完全協和音 | C, G | c_g_temp.mid | c_g_temp.mml | |
| 6度 | 短6度 | (3,2) | 8 | 5:8 | 不完全協和音 | C, G# | c_g+_temp.mid | c_g+_temp.mml |
| 長6度 | (4,1) | 9 | 3:5 | 不完全協和音 | C, A | c_a_temp.mid | c_a_temp.mml | |
| 7度 | 短7度 | (4,2) | 10 | 9:16 | 不協和音 | C, A# | c_a+_temp.mid | c_a+_temp.mml |
| 長7度 | (5,1) | 11 | 8:15 | 不協和音 | C, B | c_b_temp.mid | c_b_temp.mml | |
| 8度 | 完全8度 | (5,2) | 12 | 1:2 | 完全協和音 | C, C | c_c2_temp.mid | c_c2_temp.mml |
商用以外でしたらこのページの内容は自由にコピーして教育用にお使い下さい。 リンクも自由です。ご意見・ご質問・ご感想もお待ちしています。