
音波のイメージ図。図中の粒子は空気を構成する分子を表す
Mathematica によるアニメーション作成法
上に音波のイメージ図を示します。点は空気を構成する分子をイメージしています。 このように分子がバネのように押されたり引き戻されたりして空気中を 伝わります。音量があまりに大きいと耳から聞こえる音としてだけでなく、 体でも空気の振動を感じることが出来ます。例えば、花火大会で近くで花火を で見たときのド〜ンッという大きな音は耳だけでなく体、特に心臓に響く 空気の振動として感じることができます。
また、人間の耳には周波数特性があります。物理的には同じエネルギー、 または振幅の音を出しても人間の耳で聞いた場合には周波数によって 音の大きさが違って聞こえます。 大体の目安ですが、20000Hz以上の超音波は聞こえません。 また、20Hz以下の低い周波数も聞こえません。 例えば、0Hzの音というのは何も空気の圧力(音圧)がない、 または一定の圧力がある状態で、圧力が変化しない状態を意味します。 鼓膜に一定の圧力がかかるというのは、例えば一様に吹く風を受けるとき などです。そうすると当然体が押されるだけで音として感じないのは想像 できると思います。 実際に風の音が聞こえるのは一方向に流れる音ではなく、ヒューヒュー という音は電線などで発生するカルマン渦という不規則な渦によって 高周波が発生して風の音に聞こえるだけです。また、耳に風が当たってボコボコ 音がするのも同じように耳に当たって高周波が発生しているだけのことです。 結局直流は人間には聞こえません(エネルギーが大きかったら体が押されて 風として感じます)。 また、他の圧力一定の例としては、新幹線に乗っていてトンネルに入ったとき、 空気は1章で説明したようにやわらかいバネのようなものだから瞬時には トンネルの反対側から出て行かないために、瞬間的に圧力(気圧)が高くなり、 違う気圧に変化します。このように、影響が遠方に伝わる速度が遅いとき、 その近くだけの性質を観察すれば済むことがあります。 そのような解釈を局所現象であると言います。 さて、新幹線がトンネルに突っ込んだとき耳は聞こえにくくなっておかしくなるけど、 気圧が変わったからと言って音として感じることはありません。 一瞬耳がおかしくなる瞬間は音として感じるかもしれないけど、 それは時間的に気圧が変化する瞬間だから0Hzではありません。 トンネルに突っ込んで少し時間が経って、一定の高い気圧になったときは 0Hzと見なせます(その直後は空気がトンネルからだんだん抜けていくから気圧はゆっくり 元に戻っていくかもしれませんが)。
また、物理現象というのは急峻ではないので、0Hzに近い低周波も人間は 感じることができません。1Hz(1秒間に一回変化する音)の音というのは物理的には どのようなものかというと1秒間に1回押されてまた引き戻される風のようなものです。 当然そのようなものは音として聞こえないだろうなあと思えるでしょう。 でも、周波数が高くなっていくと音叉の振動などのように音として聞くことが できるようになります。人間にとって聞こえる音の最低周波数は20Hzぐらいだと言われます。
可聴範囲の音でも、物理的には同じエネルギーの音を出していたとしても 人間は周波数によって違った音量に聞こえます。 自分で実験したら500〜5000Hzぐらいの周波数の音は大きな音として感じるような 気がしました。このように、物理的エネルギーが同じでも周波数によって 感じる音量が変わってきます。人間が感じる音量をラウドネスレベル(LL) と言い、物理的エネルギーとの関係の周波数特性を表したグラフを ラウドネス曲線と言う(心理学的実験によって得られたもの。 フレッチャー・マンソンの等感度曲線)。
さらに、人間の音の高さの感じ方は<周波数>-<人間が感じる音の高さ>曲線 を描いたときには線形ではありません。ある周波数の音を聞いていたときに 2倍の周波数の音を出すと2倍の音の高さになったと感じます。 式で書くと最初の基準周波数をf0、nを人間が感じる音の高さ (nが1増えるてn+1となるとnのときの2倍の高さに感じる)として
fn=f0*(2^n)
となります。これはnが整数だから等比数列となりますが、 nを実数にして連続関数バージョンと見なせば指数関数となります。 <周波数>-<人間が感じる音の高さ>曲線はfn-n曲線だから 上の式の逆関数を求めると
log_{2} fn = log_{2} f0 + n
n = log_{2} fn - log_{2} f0
つまり、周波数の対数を横軸にして片対数グラフで描いたときは <周波数>-<人間が感じる音の高さ>曲線は線形となります。 このような物理量と人間の感度の関係が指数関数的になるのは他の感覚 (視覚、触覚)でもそうであり、心理学のウエーバ・フェヒナ(Weber-Fechner) の法則として知られています。次節で述べるように <音波のエネルギー>-<人間が感じる音量>特性も指数関数的となります。 この特性については次節で説明します。
もう一つ分かりやすいように目で感じる光を例に挙げましょう。 目で光を感じるということは目に入ってくる光が網膜にある受光センサー に当たり、化学反応が起きてそれを電気信号に変換して神経を伝達し、 脳に送られて処理され、光を感じます。 そのとき、同様に情報伝達速度が無限大ではないから感じるある強さ以上の 光は同じ強さにしか感じなくなる打ち切りがあるのがわかると思います。 また、そうでなくても化学反応のスピードもある強さ以上の光になったら それ以上追従できなくなって飽和するので、その特性の影響も受けて ある強さ以上の光はもうそれ以上強く感じないというのがわかると思います (それ以上強くなると光が強すぎて目や体が焼けます)。
このように大きな音を感じる限界があることはわかると思います。 実際にはそれだけでなく、あるエネルギーの音を聞いていたとき、 物理的に2倍のエネルギーの音になっても人間は2倍の音量になったとは感じません。 人間は小さな音の変化は敏感に感じ、大きな音の変化に対しては鈍感に感じるようです。 そして、実験によるとその特性は対数特性になっているようです (心理学のウェーバー・フェヒナ (Weber-Fechner) の法則)。
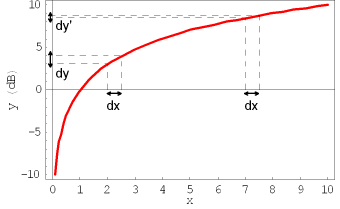
dBの説明
上の図は対数特性の説明です。横軸がエネルギーと思ってください。 そして、縦軸は人間が感じる音の大きさです。 このように音の物理的エネルギーが小さいときは変化dx に対して人間は敏感に音量の違いdyを感じますが、 音の物理的エネルギーが大きいときは変化dxに対して 人間が感じる音量dy'もわずかでしかないということを表しています。
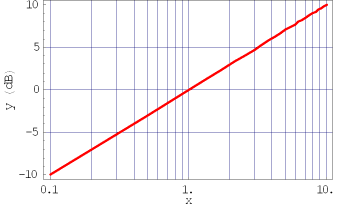
片対数グラフ
上の図のように横軸を対数目盛(log_{10} x が一定間隔になるようにした目盛) で取った片対数グラフでは直線になり、実験や論文でよく使われます。
音波のエネルギーをEとするとデシベル(dB)は
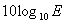
で定義されます。音波の振幅をp(音圧、圧力に対応)とするとデシベル(dB)は
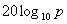
で定義されます。また、エネルギーは振幅の2乗に比例するので、比例係数をC とすると次のように書けます。
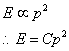
つまりエネルギーと振幅のデシベル値は次のようにグラフを上下に平行移動 しただけのものとなり相対値としては同じものになります。 つまり、エネルギーのデシベル値なのか、それとも振幅のデシベル値なのか ということを考える必要は無くなります。

ある周波数(もちろん波形は正弦波)で考えたとき、音圧レベル p の音の音量は、 人間が聞こえる最小の音の音圧レベル p_min で割った比のデシベル値で表されます。
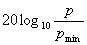
つまり、人間が聞こえる最小音の音圧を基準(リニアの値で1、デシベルだと0dB) としているので、かなり曖昧な定義だと言えます(定義によっては木の葉のざわめき のような正弦波でない波形の音を基準としてるものもあるので、さらに定義が曖昧 になります)。とはいっても、どうせ人によって聞こえ方に差があるのだから その程度の定義でもいいのかなあと思います。
また、ご意見・ご質問・ご感想もお待ちしています。