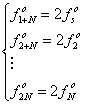音階について

2003/2/21 平野拓一（東京工業大学）

 

1. 音の高さ

 

人間はある周波数[Hz]の音を聞いていたとき、その２倍の周波数[Hz]の音を聞くと音の高さが２倍になったように感じる。言い換えると、周波数の対数を取ったものを横軸とし、縦軸に人間が感じる音の高さをプロットすると直線になることを表している。これは心理学のウエーバ・フェヒナ(Weber-Fechner)の法則として知られ、実験によって確かめられた人間の特性である。

 

1.1 標準高度

音楽で使う音の高さを世界共通で扱うために決めた特定の周波数を標準高度と呼ぶ。

古くからいろいろな標準高度が使われてきたけど、１９世紀末からはパリ会議(1859年)とウィーン会議(1885年)によって、オクターブ４のラ(A)の音を435Hzとする標準高度が代表的に使われるようになった。

しかし、現在ではシュトゥットガルト会議(1834年)で決められたオクターブ４のラ(A)の音を440Hzとする標準高度が演奏会高度やMIDIなどコンピュータを使ったDTM(Desktop Music) の基準として広く使われている。また、この基準周波数を少し高くして441Hzにすると音が全体的に少し高くなる分、音楽が明るくなったような印象を受けるので、演奏家などの注文によって440Hzでなく、441Hzや442Hz、あるいは439Hzで調律して欲しいという要望に応じて調整することもある。

 

2. 音階と等比数列

 

2.1 オクターブについて

第１節では１オクターブ上がると周波数は２倍になることを説明した。オクターブとはある音からその２倍の高さの音に聞こえる音の範囲を表している。しかし、オクターブずつ離れた音だけでは音の数が少なすぎて音楽を作るのに不十分である。そこで、１オクターブ内にいくつかの音を作り出し、それらの音に名前（音名）を与える。音楽で普通使われる音名はドレミファソラシドである。ドレミファソラシドはピアノの白鍵の音で、幹音と言われる。音楽はピアノと共に発展してきたことがわかる（そうじゃないかもしれないが）。国によって違った言い方があるが、１オクターブ内でこれらの音を使うのは西洋音楽をはじめとして世界の主流になっている。音を絶対的に指定する場合には「オクターブ４のラのシャープ(A#4)」というように指定する。普通音楽で使われるオクターブは０から８ぐらいまでである。８８鍵ピアノは27.5Hz〜4096Hzまで出せ、オクターブ０から７の途中までとなる。オクターブ０のラ(A)の音の周波数は27.5Hzであり、どうせそれより低いオクターブ-1を作っても人間にはほとんど聞こえない。オクターブ８以上の音は実際には聞くことができるが音楽ではあまり使われない。オクターブ10のラ(A)の音の周波数は後で述べる式からわかるように28160Hzであり、人間には聞こえないと言ってよい。また、MIDIでは鍵盤の数が0から127であり、ノートナンバー（鍵盤番号）127の周波数は42192.3Hzであり、人間には全然聞こえないと言ってよいから、これ以上の番号を用意する必要がない。ちなみに、このようにノートナンバーで音を指定する場合、ギターなどの弦楽器で滑らかに音の高さを変化させる演奏（ポルタメント奏法と言う）は再現できないのではないかと思うかもしれないが、そんな心配は御無用で、ポルタメント奏法を指定する命令もあるからMIDIはいろいろな楽器に対応できる。

 

2.2 12音の周波数を分配する等比数列について

 

表 1 幹音（ピアノなどの白鍵）につけられる音名

アメリカ

イギリス

C(シー)

D(ディー)

E(イー)

F(エフ)

G(ジー)

A(エー)

B(ビー)

イタリア

Do(ド)

Re(レ)

Mi(ミ)

Fa(ファ)

Sol(ソ)

La(ラ)

Si(シ)

ドイツ

C(ツェー)

D(デー)

E(エー)

F(エフ)

G(ゲー)

A(アー)

H(ハー)

フランス

Do(ド) (Ut(ユット))

Re(レ)

Mi(ミ)

Fa(ファ)

Sol(ソ)

La(ラ)

Si(シ)

日本

ハ

ニ

ホ

ヘ

ト

イ

ロ

 

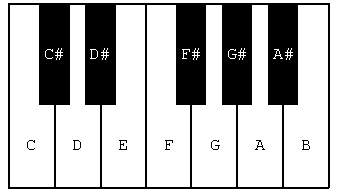
図 1 ピアノの鍵盤

 

ド・レ・ミ・ファ・ソ・ラ・シ・ドだから、１オクターブ内には全部でド〜シの全7音があると思うかもしれないが、ピアノの鍵盤を思い出してみると黒鍵もあるため実はC, C#, D, D#, E, F, F#, G, G#, A, A#, B の全12音が１オクターブ内にある（実は後で述べるように、深く考えると12である必要も無いのだが、昔から使われてきてこれが音楽の文化となったと考えられる）。どの音を基準にしても良いので、ここではAから始めてA, A#, B, C, C#, D, D#, E, F, F#, G, G# で考える。最初のAの音をオクターブ４、つまり周波数をHzとした場合、オクターブ４の他の音名の周波数はを初項とし、オクターブ５のAの音の周波数が880Hzとなるような公比の等比数列になるように１オクターブ内の周波数を分ける。

オクターブ４内の音を等比数列で書くと次のようになる。

ここで、より公比は次の条件を満たす。

よって、

一般のオクターブの音名番号の周波数を求める式を書くと、初項を変えるだけでよいので(各オクターブ内での分割の仕方は同じだから)、

                                                                         (1)

となる。はオクターブを、はそのオクターブ内の音名の番号を表す。オクターブ内の音の周波数を配分する方法を音律と言う。今の場合のように１オクターブ内の音を等比数列で配分する方法を平均律と言う。特に、１２配分しているので12平均律と言う。平均律以外にも純正律や民族音楽などで使われる音の配分の仕方がるが、現在は12平均律が世界の主流である。

２つの音名の番号の差が2のときそれら２つの音は全音（離れている）と言う。２つの音名の番号の差が1のとき、２つの音は半音（離れている）と言う。EとF、BとCの間には黒鍵が無いので半音しか離れていない。また、音符ではある音に#や♭を付けることはそれぞれ半音上げる、下げることを意味する。EとF、BとCは元々半音だから、E#やB#、F♭やC♭は存在しない（あえてその音を出そうとするなら基準周波数をずらすしかない）。また、C#とD♭、D#とE♭などは同じである。

 

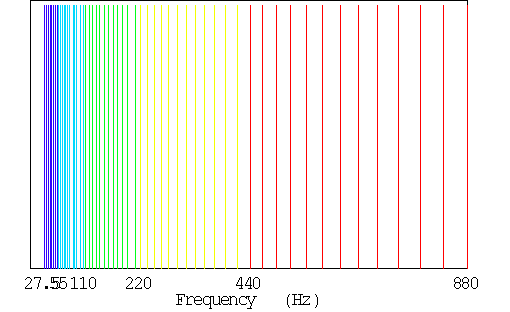
図 2 等比数列によるオクターブの分割

 

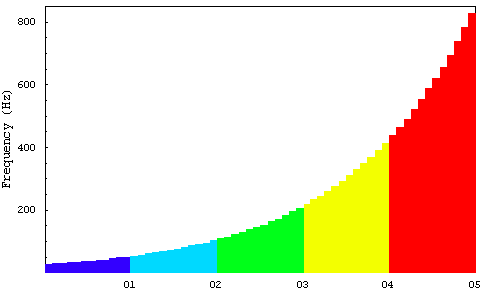
図 3 等比数列の音名番号と周波数の関係

 

波動では速度、周波数、波長の間には次の関係がある。

これからで波長を計算することができる。

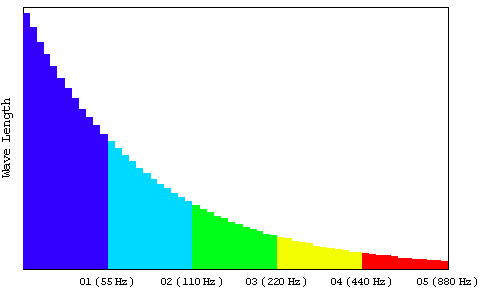
図 4 等比数列の音名番号と波長の関係

 

図 4に等比数列の音と波長の関係を示す。横軸は同じ色が同じオクターブ内の音で、オクターブ内で音名A, A#, B, C, C#, D, D#, E, F, F#, G, G# を等間隔に配置して縦軸にそれらの音に対する波長をプロットした。

ギターのフレットの間隔などはこれに対応している。例えば青のオクターブ０を例にして説明すると、ギターの弦を開放して弦を弾いたら一番低い音が鳴るが、その周波数はギターの一番下と一番上で固定された弦の振動の周波数となる。そして次にあるフレット間を押さえて弦を弾くと押さえたフレット間のギターの下側に近いフレットとギター下部で固定された弦の振動の周波数となる。

この周波数は物理の問題（偏微分方程式の境界値問題）として解くことができる。次の波動方程式（解が波動を表すから波動方程式と言う）の解が弦の振動を表す。 (m/s)は弦を伝わる波の速度（弦が無限長だったと仮定した場合のもの）を表す。ただし、は弦の変位 (m)、は時間 (s)、は位置 (m)、は弦の張力 (N)、は弦の線密度 (kg/m)である。

,                                                                                               (2)

そして上の波動方程式を、長さの弦が両端で固定されているという境界条件の下で解くと（境界値問題）、を自然数(1,2,3,…)として

                                                                                                                    (3)

という振動数の振動が起こりうることがわかる。の振動（基本周波数）が音の高さを決めるパラメータとして支配的となり、の振動（倍音）はその重み付けによって波形が変わり（フーリエ級数）、ギターやピアノなどの音色を決める。実際のギターはいくつかの弦があり、同じ開放音でも弦によって音の高さが異なる。弦をよく見ると低い音を出す弦は太くて重いことがわかる。よって、式(2)のが大きくなり、が小さくなって式(3)から弦の振動周波数が小さくなり、低い音が出ているのである。また弦の張力を変えても式(2)から周波数を変えることが可能であり、実際にそのようにしてチューニングする。式(2)を見ると同じ弦(が同じ)を使っても張力を変えれば全ての音の高さに対応できそうな気がする。数式的にはそうだが、実際には低い音用の弦を高い音用に使おうとしたら張力が大きくなりすぎ、弦が切れてしまうなど、材料の制約があるため、弦の種類で使う周波数を決め、張力で微調整するのである。

 

2.3 セント(cent)について

音楽の世界ではチューニングすることを「ピッチ（pitch, 音の高さ=音高）を合わせる」とも言う。また、２つの音の高さの差を音程と言う。これらの音の高さの違いを表すのに次の式で定義されるセント(cent)という単位を使う。

 (cent)                                                                                                    (4)

ここで、はそれぞれ音1,2の周波数である。１オクターブの差は1200セントということになる。ところで、平均律で音を分けると等比数列となり、式(4)を用いると各音の間隔はすべて同じで

 (cent)

となる。これが平均律と言われる理由で、対数を取ると等間隔になるということである。

 

2.4 なぜ音階の周波数は等比数列がいいのか？

2.4.1 １オクターブ上の高さの音は２倍の周波数になる

ある音の２倍の高さに感じる音はどの音を基準にしても２倍の周波数になっているという関係がある。それを式で表してみる。

                                                                                                                  (5)

そして、各オクターブ内を分割するということに決めると、

                                                                                                                 (6)

という関係になる。式(6)を式(5)に代入すると、

                                                                                                                 (7)

という関係が任意のに対して成立する。

今、基準周波数を決め、とすると、式(7)は

となる。

また、式(7)は任意のに対して成立するので、

                                                                                                               (8)

もまた成立する。

よって、あるオクターブ内の音はすべて他のオクターブに直すときは公比2の等比数列になっていることがわかる。しかし、あるオクターブ内での音名の周波数配分の仕方がまだ決まっていない。

 

2.4.2 オクターブ内の音の配分比は全てのオクターブ内で同じになることの証明

オクターブが公比2の等比数列になっている場合、そのオクターブ内の音の配分比はオクターブが変わっても保持されることを証明する。オクターブ内のの配分比をを、を1としてそれぞれとすると、

 

・・・

・・・

 

配分比とそのオクターブの周波数間隔を使ってそのオクターブ内の音は次のように書くことができる。

                                                                                            (9)

さて、ここで「オクターブの音」と「オクターブの音」の関係に着目する。後者の周波数は前者の２倍になっているので、

上の式に式(9)を代入すると

というとの関係が得られ、オクターブを変えても配分比の関係は保持される。

 

2.4.3 基準音を変えても同じ配分比になるようにする（自己相似形）

さて、今までの議論ではあるオクターブを決め、オクターブ内で音を割り当てるということをしていた。オクターブの基準はどこにしてもいいはずである。よって、オクターブ内の他の音を基準にしたときにも前節の配分比が保持されるような条件を導出する。

まず、を基準としてオクターブを決める。

上のを基準とした音階では、がオクターブの初めの音となる。はそのオクターブ内での配分比を表す。この節の最初に要求した、「オクターブの基準音を変えても配分比が等しくなるようにする」というのは式で書くとが要求されるということである。

を基準とした音階では式(9)よりは次のようになる。

ここで、だから、

高校で習う漸化式の解法より、

                                                                                                           (10)

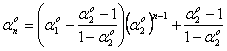
式(10)を式(9)に代入すると、

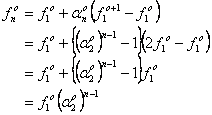
よって、基準音を変えてもオクターブ内の音を同じ比で配分するという条件から式(1)と同じ等比数列が得られた。このように等比数列は音の基準を変えても自己相似形になる。また、今は1音だけずらして相似形になるような条件を求めたが、何音ずらしてその条件を導いても結果は同じになる。このように、自己相似になるという条件から等比数列を導いたので、自己相似になるような周波数配分は等比数列しかありえない。

 

2.4.4 Weber-Fechnerの法則より、等比数列を使うと人間が感じる音の高さをオクターブ内で等分配するという説明

2.1.1節である周波数の音が２倍になると、音の高さも２倍になったように感じるという説明をした。

さて、ここであるオクターブ内に１２個の音を作るとする。そのとき音をどのように配分すれば一定の高さで音が高くなると人間は感じるだろうか。今、オクターブ基準音のAについて考えてみると、オクターブ0のAの音は27.5Hzとすると、その２倍高い音に感じるオクターブ1のAの音は27.5×2=55Hzとなる。さらにその２倍高い音に感じるオクターブ3のAの音は55×2=110Hzというように、２倍ずつ大きくなっていく。これは心理学のウェーバー・フェヒナ(Weber-Fechner) の法則として知られている。式で書くとオクターブのAの音の周波数は

                                                                                                             (11)

となる。つまり、等比数列となっている。頭で人間が感じる音の高さと周波数の高さの関係を想像した場合、式(11)ではなく、となるのではないかとも考えられるが、心理学的実験で式(11)が成り立つことが実証されている。人間の感覚という量を扱うのだから、そこは心理学的実験によって求めるしかない。

さて、式(11)では２倍高く感じる音について議論したが、そのオクターブ内で１２個の音を生成するとき、どのように周波数を配分したら均等に音が高くなっていくと感じるか考えてみる。式(11)の結果から式(1)のようにそのオクターブ内でも等比数列となるように周波数を配分すれば人間は音が均等に高くなっていくと感じるのではないかと予想できる。実際そうであり、普通音楽で使う音階の周波数は式(1)で表される。さらに2.1.3節で説明したように自己相似形となるため、どのオクターブを基準にしても、オクターブ間にまたがっていろいろな音を使っても、転調しても都合よく感じる音の高さの間隔が均等になっているのである。これが等比数列で音の周波数を分配すると都合良い理由である。

 

2.4.5 等比数列の指数関数的性質とデシベル

式(1)では整数だからの等比数列であるが、が連続量だったと仮定してみよう。すると式(1)はの指数関数となる。つまり、対数を取って周波数をデシベル表示すれば音の番号と周波数の関係は線形となる。

 

3. 等比数列以外の音階

 

2章では等比数列でオクターブ内に音を配分して平均律で音階を作り上げたが、もちろん他の配分の仕方（音律と言う）も考えられる。

例えば、全１２音階中の主要な完全五度と長三度が和声的に純正に響くように、各音間の音程を単純な整数比で定めた純正律がある。平均律と比べると主要３和音がとても美しく響くが、１つの調でしかその効果が得られず、転調すると和音が濁ってしまう。他にもアラビア風音階などのさまざまな民族音楽で使われる音律（音の周波数の配分方）がある。MIDIではスケール・チューン機能を使って各音の平均律からの差（単位はセント）を指定していろいろな音律にチューニングすることができる。

 

3.1 等差数列で音階を作ったら？

ここではオクターブ内で音の周波数が等差数列になるように配分したらどうなるか考えてみる。音の配分を式(1)ではなく、次の式を用いて各オクターブ内で等差数列になるように配分する。

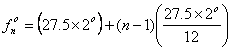                                                                          (12)

 

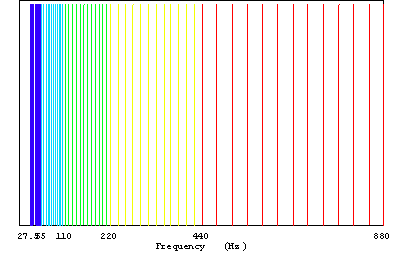
図 5 等差数列によるオクターブの分割

 

図 5に等差数列でオクターブ内の音の周波数を配分した図を示す。そのオクターブ内では等差数列となっているが、どの音を基準にしても良いので、例えば曲の中で転調した場合やオクターブをまたいで演奏した場合にどのようなことが起きるか考えてみる。例えば、オクターブ内の最初の音ではなく、他の音を基準にして音階を作り直すとしたら、図 5を見てわかるようにもうすでにその中で等差数列になるという規則が崩れてしまう。よって、その新しい音階では順番に音を出していくと一定の高さで音が上がるという規則が無いだけでなく、音の上がり方がバラバラに崩れてしまう。等比数列で配分した場合は他の音を新たなオクターブの基準にしても、またそのオクターブ内で等比数列の分割となっており、自己相似形になっていからオクターブが変わっても、転調しても違和感がない。この理由からも等比数列による分割が曲を作るのに最も都合よいのではないかと想像できる。

 

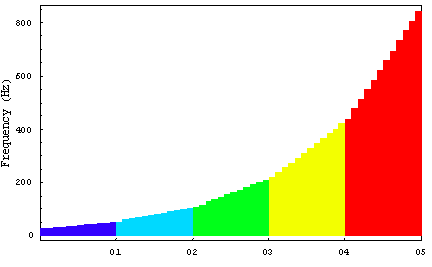
図 6 等差数列の音名番号と周波数の関係

 

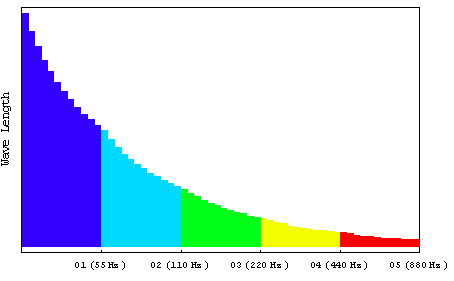
図 7 等差数列の音名番号と波長の関係

 

参考として等差数列でオクターブ内の音の周波数を分割したときの音名番号と周波数、音名番号と波長の関係をそれぞれ図 6、図 7に示す。グラフの形を見ても、やはり図 3、図 4のような等比数列で分割した平均律の方が自然なのではないかと思われる。

 

4. なぜ１２音なのか

 

さて、2,3章の議論でオクターブ内の音は等比数列で配分するのが都合良い感じがするのはわかったと思うが、なぜオクターブ内に１２個の音を作っているのだろうか？なぜ１０音や１６音などの他の数ではないのだろうか？これは2章の議論を見ればわかるように１２音である必要はない。昔から発展してきた音楽はだんだん人間の感性に合うように１２音になったものと考えられる。だから音楽で使う音は１２音である必要はないし、連続した全ての高さの音を使った音楽も考えられる。また、１２音を使う音楽では、それらの１２音も対等に扱わずに、ピアノでは７個の白鍵と５個の黒鍵にわけて使っている。そしていくつかの音を抽出して音階をつくり、音階の種類によっても調にわけられる。長調ならば曲が明るい感じがし、単調なら暗い感じがするというものである。

今までは音の物理的考察から始まり、心理学のウェーバー・フェヒナの法則を使って人間の音の感じ方も取り入れてなるべく論理的に、物理的に考察してきたが、長調、単調などの話になってくるともう物理の問題として考察できなくなり、心理学を使っても非常に難しい問題となる（まだ物理的、心理学的に考察できる課題で取りこぼしたものもあるが）。これ以上は人間の感性がどのようなものかという議論になってくる。これを扱う学問が「音楽」（音学でなく、楽しむという気持ちが出ているところがうらやましい）であり、私の能力を超えるのでこれ以上は音楽の専門家にお任せする。まだ物理学、心理学、音楽の各学問分野の間にギャップがあり、完全に説明できていないが、うまく連携して発展しているような気がする。いずれ物理学で脳の情報処理の仕組みが解明されれば、全てが繋がって説明できるかもしれない（にちがいない）が、まだかなり先の話になりそうである。私は下位の層で物理的考察をするのが専門であるが（実は電界解析が専門だからちょっと脱線している）、音楽は大好きであり、このような考察をして少しでも音楽家、作曲家、ミュージシャン、アーティスト、芸術家の役に立つことができれば嬉しい。