Scale Tuning

2003/3/23 Takuichi Hirano

周波数を求める関数（平均律）

[Input]
オクターブ
音 (c,c#,d,d#,e,f,f#,g,g#,a,a#,b)

In[1]:=

ABCToNumOfHalfTone[ABC_] := Which[ ABC == "C" || ABC == "c", 0, ABC == &q ... ; FreqTemperament[OctABCList_List] := Map[(FreqTemperament[#[[1]], #[[2]]] &), OctABCList] ;

周波数を求める関数（純正律）

基準周波数は平均律で決める。
基準音から２オクターブ分までサポート

[Input]
基準音のオクターブと音名
と
オクターブ
音 (c,c#,d,d#,e,f,f#,g,g#,a,a#,b)

In[4]:=

FreqJustIntonation[OctaveStd_, ABCStd_, Octave_, ABC_] := Module[{r = 2^(1/12)}, (* 純正律 (just ... ABCList_List] := Map[(FreqJustIntonation[OctaveStd, ABCStd, #[[1]], #[[2]]] &), OctABCList] ;

Difference Between Temperament and Just Intonation

In[6]:=

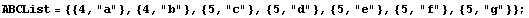
ABCList = {{4, "a"}, {4, "b"}, {5, "c"}, {5, "d"}, {5, "e"}, {5, "f"}, {5, "g"}} ;

In[7]:=

FreqTemperament[ABCList]

Out[7]=

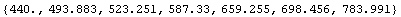
{440.`, 493.8833012561241`, 523.2511306011972`, 587.329535834815`, 659.2551138257397`, 698.4564628660077`, 783.9908719634988`}

In[8]:=

FreqJustIntonation[4, "a", ABCList]

Out[8]=

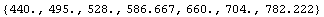
{440.`, 495.`, 528.`, 586.6666666666666`, 660.`, 704.`, 782.2222222222222`}

In[9]:=

g1 = ListPlot[FreqTemperament[ABCList], PlotStyle -> {AbsolutePointSize[8], AbsoluteThickn ... 1, 7}, {440, 880}}, Frame -> True, Axes -> None, DisplayFunction -> $DisplayFunction]

[Graphics:HTMLFiles/index_9.gif]

Out[13]=

-Graphics -

Scale Tuning Data for MIDI
Roland SC-88VL Manual p. 86, p. 80

In[14]:=

DecNumberToHexString1[n_] := Module[{}, Which[ n == 10, "a", n == 11, "b" ... tring1[hex[[2]]] ] ; CentToMIDIScaleTuningData[lis_List] := Map[CentToMIDIScaleTuningData, lis] ;

In[26]:=

CDEList = {{4, "c"}, {4, "c#"}, {4, "d"}, {4, "d#"}, { ... uot;} &), CentToMIDIScaleTuningData[Round[1200 * Log[2, Scale[1]/Scale[0]]]] ] ] , -1 ] ] ] ;

**** 平均律からのずれのピッチ(セント値) ****

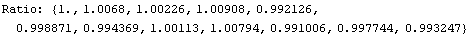
Ratio: {0.9999999999999998`, 1.0067992668604728`, 1.0022610579078817`, 1.0090756983044573`, ... 1298906275254`, 1.0079368399158988`, 0.9910059291689338`, 0.9977440429416646`, 0.993246650961839`}

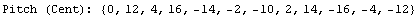
Pitch (Cent): {0, 12, 4, 16, -14, -2, -10, 2, 14, -16, -4, -12}

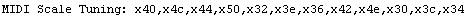
MIDI Scale Tuning: x40,x4c,x44,x50,x32,x3e,x36,x42,x4e,x30,x3c,x34

Converted by Mathematica  (March 29, 2003)