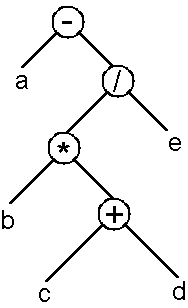
図1: 二分木
説明を読めばわかるが、実は人間はコンピュータにとって一番扱いにくい 内挿表現を使っているのである。 人間は数式をざっと見ただけで演算の順番がわかるが、コンピュータにとって そのようなことは苦手である。 (もちろん人間も小学生・中学生のときに訓練させられたから慣れているだけ なのだが)
a-b*(c+d)/e 式(1)これは私達が普通に使う表現であり、算数・数学の授業で計算法を習ってきたので 人間にとってはパッと見ただけで計算の順序が非常にわかりやすい。 しかし、コンピュータでこのような一般の数式の計算をするプログラムを作ろうと 試みてみるとわかるのだが、計算順序は前から順番に行われる訳ではないので 非常にプログラムを作りにくい。 そこで、次の二分木構造を考えよう。

図1: 二分木
図1 は式(1)の二分木を書いたものである。 また、この図は言語処理では解析木とも呼ばれる。 この表現にすると木の葉の方から解析していけばよく、 演算の順番が明らかとなってコンピュータでも容易に処理が可能である。 実際には根(図1 では一番上)から見ていって奥の葉の方から評価していく 再帰呼出し (recursive call) プログラムを書けばよい。 二分木はリンクドリストを用いてインプリメント可能だが、 紙に書くときは場所を取るので次の3つの前置表現 (prefix form) と後置表現 (postfix form)、関数表現を考える。 しかし、ここで言いたいことは二分木で表現できたら内挿表現、 前置表現、後置表現、関数表現のいずれの表現に変換することも 容易だということある。
(- a (/ (* b (+ c d)) e)) 式(1.1)この式(1.1) から二分木を作ることもまた容易であり、表現もコンピュータ 内部で扱う表現に適している。
(a ((b (c d +) *) e /) -) 式(1.2)これはほとんど前置表現と等価であり、書かれている順番が違うだけで本質的には変わりない。
ここでは、オペレータに次のような関数名を対応させて、 式(1) の関数表現を作ると式(1.3)を得る。
| 演算子 | 関数名 | 定義 |
| + | plus | plus(a,b)=a+b |
| - | minus | minus(a,b)=a-b |
| * | mult | mult(a,b)=a*b |
| / | div | div(a,b)=a/b |
minus(a,div(mult(b,plus(c,d)),e)) 式(1.3)これはコンピュータプログラミングの関数呼出しそのものの形をしている。 少し書き方が違うだけで、前置表現と本質的に変わりはない。