1章 なぜ興味を持ったのか

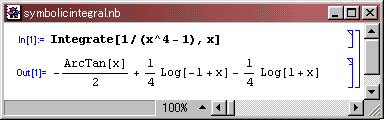
図1: MATHEMATICA の不定積分の例

僕は中学のときに2次方程式の因数分解を習ったときに FOR 文で適当な 値を入れてみて因数分解をする BASIC プログラムを作りました （後になって、2次方程式の解の公式を使っていとも簡単に因数分解できることを 知ったのだけど・・・）。 ちなみに、当時持っていたパソコンは Panasonic の MSX2+ でした。 中学の頃は因数分解は「パズルみたいで面白い」という人もいたけど、 確かにそうだったけど、僕にはパズルみたいな試行錯誤的なものは スッキリしなくて気持ち悪くて仕方ありませんでした。 論理的で誰がやっても同じになるようなアルゴリズムを知りたかったのです。

そして、大学に入学したとき、自動的に数学の計算をするプログラムを作りたいと 思っていました。 計算するというのは大学入試のためにもよく勉強した記号的 (symbolic) に sin(x) cos(x) を積分したりする（つまり不定積分）高度な計算です。 記号的に積分するのは色々な公式を覚えなければならず、かなり慣れが必要です。 でも、基本的にやってることは公式を使うだけだからプログラムは難しそう だけどコンピュータにできないことはないだろうと思っていました。 そのことを大学（名工大、電気情報工学科）の新入生歓迎企画の合宿で 将来どんな研究をしたいか先生に聞かれたときに話してみたら、 「"Mathematica" っていうソフトだったらできるよ」とあっさり言われて しまい、ビックリしました。そのときは「本当にそんな凄いソフトあるのか？」 と思いつつ大学１年のハードな教養課程に突入し、時間が流れていきました。

大学に入るとさすがに周りにはプログラムが出来る人が多かったです。 僕も早速 C 言語を勉強しました。 大学の授業の「プログラミング入門」で Pascal を教えてもらった M 尾先生が 講義中にチョロっと二分木構造について触れ、これは使えると思って 数式を入力すると答えを出す C プログラムを書きました。 もちろんそれは記号的に計算するのではなく、単に式を再帰的に解析・評価して数値を返す だけのプログラムだったけどうまく動いてすごく嬉しかったです。 始めての C 言語プログラムにしては重い内容だったけど、それで C 言語の難関 とも言われるポインタは完全に理解できました。

大学2年のあるとき、数学好きだった僕にクラブ（ハム・オーディオ研究会） の先輩が「Mathematica が手に入ったから貸してあげるよ」と言って貸してくれました。 喜んで微・積の教科書を取り出して大学で習う複雑な積分を試してみたところ、 Mathematica は全ての例題を解いてしまって感動しました。そして講義で習った 関数論の「留数」問題や、電気系基礎数学や制御工学で習った「ラプラス変換」 の問題まで難なく記号的 (symbolic)に解いてしまいました。 しかも、テイラー展開や固有値・固有ベクトルの問題まで記号的にやってしまいます。 すごくビックリしました。 大学の実験レポートは Mathematica のおかげでかなり楽できた気がします。 数学の意味を理解していない人が使うのは良くないけど、 理解してる人が電卓と同じような感覚で使うのは非常に仕事の効率が上がっていいことだと思います。

大学 4 年になって研究室に配属され、専門は「電磁界理論」になりました。 そして、 ICT (Improved Circuit Theory) の研究をしたときに、長くて複雑な積分が 出てきて Mathematica を利用してうまく計算することができました。 もし Mathematica がなかったらその研究には遥かに時間がかかったことは確実です。

そして、大学院になって東工大に来ました。専門は変わらず「電磁界理論」です。 今もモーメント法とか有限要素法をやっていて、 Mathematica が大活躍しています。

そんな数式処理ソフトの動作原理を調べてみたかったので調べてみました。 ここでは数式処理ソフトの原理のレポートを紹介します。