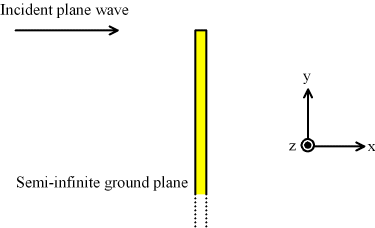
図1: 座標

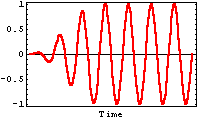
図1 に示すようにy軸上に半無限(y=-∞〜0)完全導体板が置かれている。 導体板は波長に対して十分に薄い。 z方向には一様な構造になっている(2次元問題)。 左方向(-x方向)から平面波を入射させたときの電磁波の 回折(diffraction)のアニメーションを示す。 電波と光は共に電磁波の一部だが、電波は波長が長いため、回折という現象が顕著となる。
図2 は入射平面波の波形の時間変化を示す。
以下では入射平面波がTE問題とTM問題のそれぞれの場合に分けて電界の強さの アニメーションを示す。 電磁波は電界と磁界があり、完全導体(金属)に当たったときのそれらの振舞いが 違うための、水の波の回折よりも少し複雑となる。 完全導体上では電界の接線成分が0になるということを考えるとTE問題とTM問題の 振舞いの違いを想像しやすい。
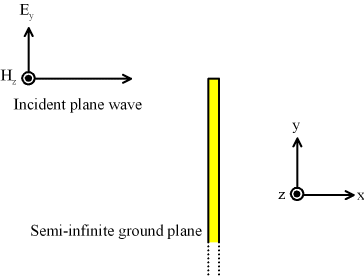
高周波と低周波の回折の違い
[考察]
回折により導体板の裏側によく回り込んでいる。 x-z平面を地面、+y方向を鉛直上方向と見なすと、 これは垂直偏波(電界が鉛直方向)に相当し、移動体通信で用いられる。
例えば、携帯電話などのアンテナの導体棒は地面に垂直にして用いる。
山やビルを上の問題の半無限導体板と見なすと回折の恩恵に預かることができ、 電波が直接到達しないところでも通信できることがわかる。

[プログラムソースファイル (FORTRAN90)]
| 説明 | ファイル名 |
|---|---|
| メインルーチン | main.f90 |
| モジュール | module.f90 |
| 初期化 | init.f90 |
| モデリング | model.f90 |
| 電界更新 | efield.f90 |
| 磁界更新 | hfield.f90 |
| 境界条件 | boundary.f90 |
| 吸収境界条件 | abc.f90 |
| 波源 | source.f90 |
| 出力 | output.f90 |
| 入力ファイル例 | input.dat |
| 視覚化用 Mathematica ファイル | visualize.nb |
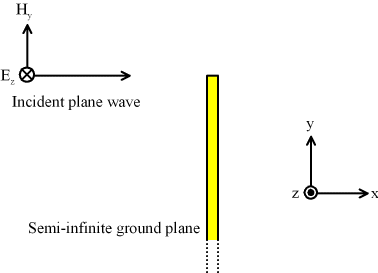
[考察]
回折して導体板の裏に回りこんでいるが、TE問題程ではない。
x-z平面を地面、+y方向を鉛直上方向と見なすと、
入射波の電界は地面に平行で鉛直成分を持たないので水平偏波と言われ、
固定されたもの同士の通信に使われる。
例えば、東京タワーから放射される電波は水平偏波であり、
それを固定されたテレビ用のアンテナで受信する。
テレビ放送の受信アンテナは屋根の上などにあり、導体棒が水平に置かれて
いることからも水平偏波を受信していることがわかる。
[プログラムソースファイル (FORTRAN90)]
| 説明 | ファイル名 |
|---|---|
| メインルーチン | main.f90 |
| モジュール | module.f90 |
| 初期化 | init.f90 |
| モデリング | model.f90 |
| 電界更新 | efield.f90 |
| 磁界更新 | hfield.f90 |
| 境界条件 | boundary.f90 |
| 吸収境界条件 | abc.f90 |
| 波源 | source.f90 |
| 出力 | output.f90 |
| 入力ファイル例 | input.dat |
| 視覚化用 Mathematica ファイル | visualize.nb |
なお、これらの問題はA. Sommerfeldにより解析解が与えられている (A. Sommerfeld, "Rigorous Solutions of Certain Diffraction Problems," OPTICS DIFFRACTION FROM THE CONDUCTING EDGE, New York: Academic Press, pp. 247-272, 1954)。 解析解とFDTD法による数値解法は一長一短あるが、なんとなくやってみようかな と思ったときにできる手軽さがFDTD法のいい所ではないだろうか。