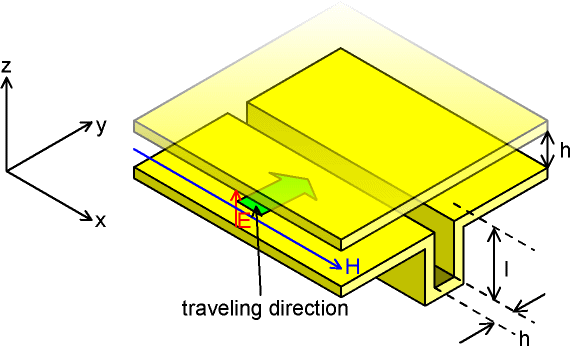

溝が無い場合、左下から進行して来るTEM波は反射することなく右上に 向かって進行していく。これから、溝があるとどうなるか見てみる。
以下のグラフィックはFDTD法を用いて計算し、y-z平面内の磁界の2乗を示す。
| 溝の深さ l | アニメーション | 説明 |
|---|---|---|
| 溝が無いとき | View | 反射しないで進行する |
| 1/8 波長 | View | 溝で反射波が生じる |
| 1/4 波長 | View | 入射波と溝で生じた反射波(溝から右に進行しようとする波)は逆相となり、 定常状態では右側に波が進行しなくなる |
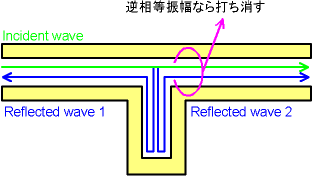
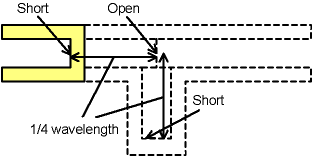
上の「溝の深さ l の影響」でl=1/4波長のとき、定常状態では 入射波と 溝で生じた反射波 (Reflected wave 2) は逆相となり右側では打ち消されて波が進行しなくなる。 導波路を基本モードしか通さないように使っている場合は 電気的にはあたかも入射側から見たとき、 溝の短絡部から1/2管内波長おきの場所では短絡されているように見える (定在波分布を想像すればそう見なしても構わないことがわかる。 溝との繋ぎ目では少し複雑な分布をするために厳密ではないが、 直線の導波路部分は基本モードだけ進行しているのでそれでうまく説明できる)。
定性的にl=1/4波長のときに透過波が小さくなることの説明をする。まず、線路と溝の交差部に到達した入射波の位相を基準として、溝からの反射波の交差部に到達する反射波の位相がどのように変化するか見てみよう。まず、l=1/4波長なので、行きと帰りで1/4波長ずつ、つまり1/2波長進行する分の位相遅れがあり、180°遅れる。また反射するときに短絡終端なので、180°位相がずれる。合計360°位相がずれて反射してくる。つまり同位相で加わることになる。すると、透過波も同位相で足しあわされてしまうかと思うかもしれないが、そうではない。
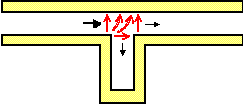
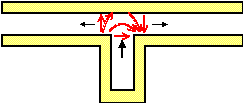
上の図を見てみよう。左の図の赤い矢印は交差部への入射波が入射したときの電界の様子を示している。右の図では溝からの反射波が導波路に戻っていく様子を示している。溝から導波路に戻るときは左右の導波路で位相が180°変わるのである。したがって、交差部に同相で反射してきても、右側では透過波と逆相になっている。このようにして溝より右側では波が打ち消されるのである。
これをチョーク (Choke) 構造と言い、機械的な短絡が難しいときに 使われる構造である。(Chokeとは「ふさぐ」と言う意味である。 電気回路の整流用にはチョークコイルというのが使われることがあり、 直流以外の交流を「しめる」という意味である。 エンジンのチョーク弁は空気の流れをふさぐものである) ただし、チョーク構造は周波数特性を有する (原理的に溝の深さ l がλ/4+nλ/2、となるような周波数でしか所望の動作をしない。 ただし、 n は整数)。 よって、どんなときでもチョーク構造を使えば良いというものではなく、 機械的に短絡できるならば機械的に短絡した方がよい。
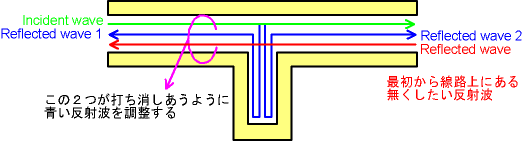
反射波を無くすには上のチョークの説明を応用して考えると、 溝を掘って丁度反射波と 同じ振幅で逆相の反射波 (Reflected wave 1)を作り、 本来の反射波 がそれによって打ち消されるようにすればよい。 実際には溝による反射波 (Reflected wave 2)もまた 入射波に加わって先に繋がる回路に入射し、 入射側に返ってくる反射波も変えることになる。 そのような多重反射の影響を考慮したいときは伝送線路モデル を用いればよい(参考資料:Microsoft Word ファイル, PDF ファイル)。 ここでは説明を簡単にするため多重反射を無視して考える。
溝による反射波 (Reflected wave 1)の振幅は変えられないので、 溝の深さ l を変えるだけでは整合を取れないだろうことは予想できる。 従って、実際には溝の負荷からの距離と深さを両方変えるようにする。 このように整合を取るために作った構造をスタブ (Stub)と言う。 スタブももちろんチョークと同じように周波数特性を持つため、 なんでもかんでもスタブで整合を取ろうとするよりは、各ブロックで 出来る限り整合を取ろうとする方が一般的には周波数特性が広帯域となる。
ここまでスタブの説明として平行平板線路に設けた溝構造を例に挙げたが、 もちろん原理的には線路は平行平板でなくてもどんな線路でも構わない。