電磁波の散乱 (Scattering)

様々な散乱体による散乱を見てみよう。

  構造／コメント FDTDシミュレーションによるCG
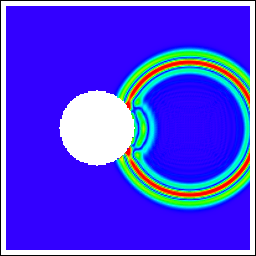
円筒導体

半径: 1.5λ

波源: 線磁流源, 円筒導体中心から6.25λ
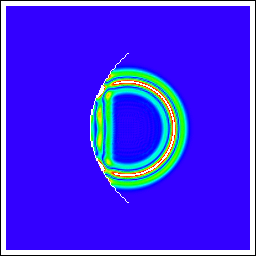
円筒誘電体

半径: 1.5λ; 比誘電率: 3

波源: 線磁流源, 円筒導体中心から6.25λ
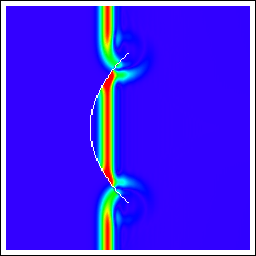
２次元放物体

パラボラ開口半径: 3λ

焦点に置かれた１次放射器から放射される円筒波を平面波に変換（送信）。
パラボラ正面から入射する平面波を焦点で位相を揃えて合成（受信）。
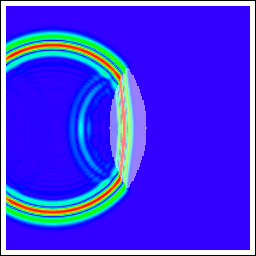
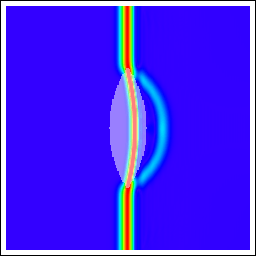
誘電体レンズ

si=∞ （点波源を平面波に変換）

薄肉レンズの式:
f=3λ, so=3λ(ガウスのレンズ公式: 1/so+1/si=1/f), R1=4.5λ, R2=-4.29λ, 比誘電率: 3

c.f.) E. Hecht, ヘクト光学I, 式(5.16)-(5.17), p.242, 丸善

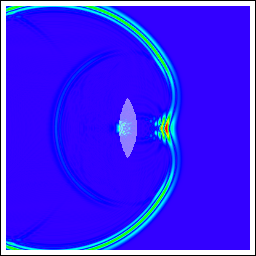
si=∞ （平面波を焦点に結ぶ）

薄肉レンズの式:
f=3λ, so=3λ(ガウスのレンズ公式: 1/so+1/si=1/f), R1=4.5λ, R2=-4.29λ, 比誘電率: 3

c.f.) E. Hecht, ヘクト光学I, 式(5.16)-(5.17), p.242, 丸善

si=6λ （点波源を焦点に結ぶ）

薄肉レンズの式:
f=3λ, so=6λ(ガウスのレンズ公式: 1/so+1/si=1/f), R1=4.5λ, R2=-4.29λ, 比誘電率: 3

c.f.) E. Hecht, ヘクト光学I, 式(5.16)-(5.17), p.242, 丸善
Copyright(c) 2008 Takuichi Hirano, All rights reserved.

Back