2008.11.4 平野拓一
コンピュータを利用して数値的に値を評価する手法。例えば、不定積分が求まらない場合に区分求積で定積分値を求めるなどである。数値計算はコンピュータを利用するが、一般に、
のは誰でも望むことである。しかし、上記の2つは相反する要求となる。上記2つの要求を満たすようなアルゴリズムを開発するのが数値計算の専門家の仕事となる。
数値的に得られるデータは離散的である。その間の値、あるいはその外の値を知るためにサンプリングした離散値から連続関数を生成することがしばしば行われる。そして、生成した連続関数から間の値を予測することを補間(interpolation)、サンプリング範囲外の値を予測することを補外(extrapolation)と言う。

n点ある場合はn-1次の多項式で近似する方法。
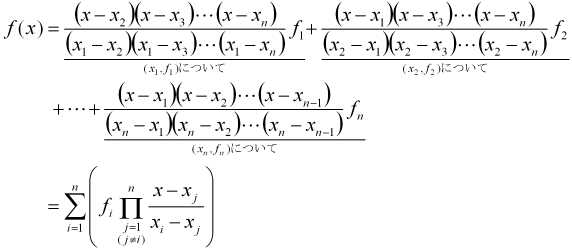
(作成中)
有理関数で近似する方法。ラグランジュ近似では表現不可能な、極(n次の極とは、無限大に発散するが1/x^nで表すことができる特異点)がある関数を近似するのに精度が良い。
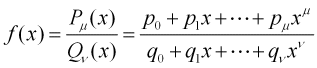
上式の未知数の数はp0,…pμのμ+1個と、q1,…qνのν個(q0は定数項のp0/q0を表すためなので、任意[例えば1]に選べる)で、合計μ+ν+1個である。よって、サンプル点がn個の場合はn=μ+ν+1と選べばよい。上式の係数は次のように求めることができる。
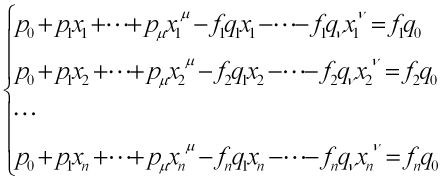
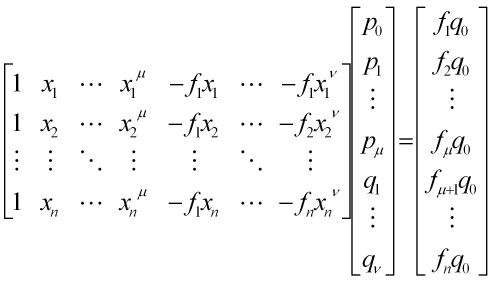
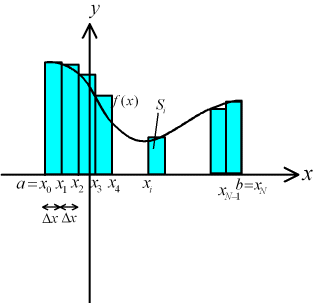
まず、1次元積分について説明する。
長方形の面積の和。
[参考文献]
・num_diff_int.pdf (数値微分と数値積分
by T. Hirano)
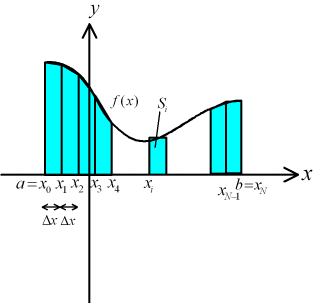
台形面積の和。
[参考文献]
・num_diff_int.pdf (数値微分と数値積分
by T. Hirano)
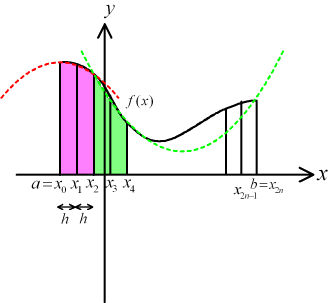
3点を用い、2次曲線で補間して面積を計算する。滑らかな関数で精度が高い。
[参考文献]
・num_diff_int.pdf (数値微分と数値積分
by T. Hirano)
ルジャンドルの多項式の直交性を利用した不等間隔数値積分。被積分関数が2n-1次の多項式で表現されるならば、分点数をn点以上にすると誤差は0となる。有限要素法では滑らかな関数を積分するので、よく用いられる。
[アルゴリズム]
![]()
を求めたいとする。積分範囲は-1~1であるが、最後に積分範囲の変換式を示すように、これでも一般性を失わない。f(x)を2n-1次の多項式とすると、n次のルジャンドルの多項式Pn(x)で割った商Q(x)と剰余R(x)で表す。
![]()
ところで、ルジャンドルの多項式は互いに直交している。
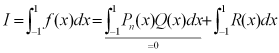
なぜならば、Q(x)はn-1次であるから、
であり、直交性から上式の下線の積分は0となる。
求積を行う際、下記のように等式で結べるとする(f(x)は2n-1次の多項式であると仮定しているから)。
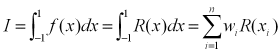
Iを求めるためにはR(x)を求めなければならないように見えるが、![]() より、Pn(x)の0点
より、Pn(x)の0点![]() をサンプリング点に選ぶと
をサンプリング点に選ぶと![]() となる(R(x)を求める必要がない)。
となる(R(x)を求める必要がない)。
さて、残るはwiはどのような値であるか定めることである。上の右2式より、
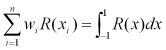
R(x)は任意のn-1次の多項式に対して成り立たなければならない。R(x)として、P0, P1, ..., Pn-1のn個の関数を選ぶと次のn個の連立一次方程式が得られる。
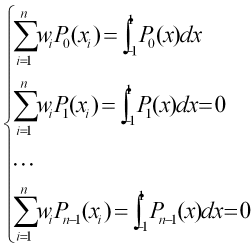
w1, ..., wnは上式を解くと求めることができる。これでn次の公式が得られた。
例として、n=3の場合のxiとwiを示す。
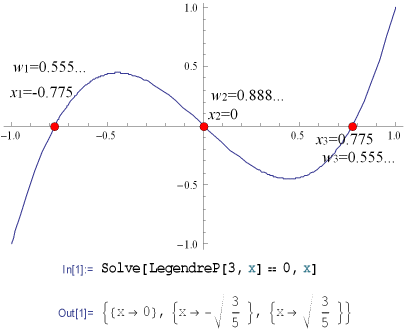
積分範囲をa~bにするには次のように座標変換するだけでよい。
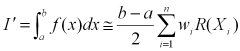
ただし、
方形領域であれば、多次元への拡張も容易である。
[参考文献]
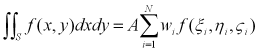 (※)
(※)点が多面体の内部か外部かを判定するだけで良いので、多次元積分に非常に威力を発揮する。
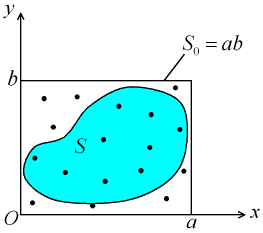
x,yを一様分布に従う確率変数とし、xは[0,a]、yは[0,b]の乱数を発生させる。十分多いN回試行し、(x,y)がS内に落ちた個数Niとする。すると、積分領域の面積は次の式で表すことができる。
![]()
より一般の関数の積分は次のようになる。
![]()
ここで、![]() はS内での関数f(x,y)の平均値であり、次式で求めることができる。
はS内での関数f(x,y)の平均値であり、次式で求めることができる。
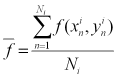
ここで、(xin,yin)はS内に落ちた点の座標を表し、∑は内部に落ちた点について和を取ることを意味している。