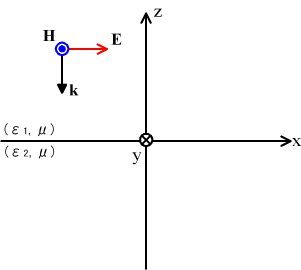
以下の問題では、z>0に誘電率ε1、透磁率μの媒質が、z<0に誘電率ε2、透磁率μの媒質が、x-y平面を境に接している状況を考える。ここで、波数は k1=ω√(μ ε1), k2=ω√(μ ε2)、界インピーダンスは η1=√(μ/ε1), η2=√(μ/ε2)となる。

ここでのアニメーションでは電界の2乗の強さ(エネルギー)を示す。
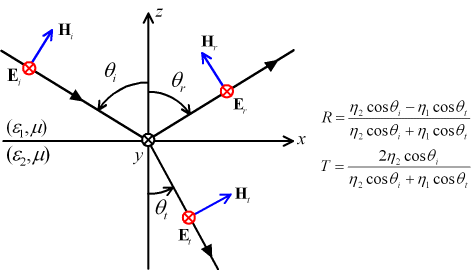
入射波の波数ベクトルkiと媒質の法線ベクトルn^を含む面を入射面(incident plane)と呼び(この問題では入射面はx-z平面)、入射波の電界が入射面に垂直で、入射面と直交しているので、この入射波の偏波を直交偏波と呼ぶ。電界が入射面に直交しているのでTE波(transverse electric wave)またはS波(ドイツ語の「垂直」を意味するsenkrecht)、あるいは磁界が入射面内にあるからH波とも言われる(単なる定義である)。
位相整合条件(位相整合条件の説明)により、反射角θrは入射角θiに等しい(θi=θr)ことがわかる(反射の法則)。また、
ε1>ε2の媒質条件のとき、入射波は透過しないで全て反射する全反射(total reflection)がおきる。 入射角がある角度をこえると常に全反射となる。全反射となる最小の入射角を臨界角(critical angle) θc=arcsin(k2/k1)=arcsin(sqrt(ε2/ε1))と言う。全反射は完全導体による反射とは異なり、媒質2の中にもしみこむが、エネルギーは-z方向に向かって指数関数的に減衰し、-z方向にはエネルギーは進行しない。
ここでのアニメーションでは電界の2乗の強さ(エネルギー)を示す。
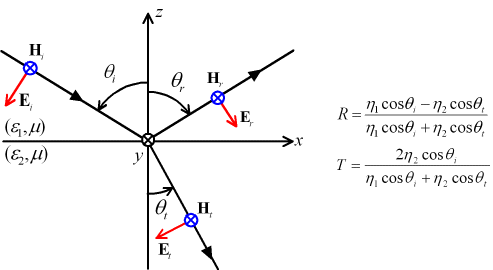
入射波の電界が入射面内にあり、入射面に平行なので、この入射波の偏波を平行偏波と呼ぶ。磁界が入射面に直交しているのでTM波(transverse magnetic wave)またはP波(「平行」を意味するparallel)、あるいは電界が入射面内にあるからE波とも言われる(単なる定義である)。(直交偏波、平行偏波)、(TE波、TM波)、(E波、H波)の呼び方は主に電磁波の分野で使われ、(S波、P波)の呼び方は光波の分野で使われることが多い。
平行偏波の場合、反射波がなくなり、入射波が全て透過していく角度、ブリュースター(Brewster)角 θb=arcsin(sqrt(ε2/(ε1+ε2)))が存在する(直交偏波には存在しない)。ブリュースター角は媒質条件によらずに存在する。
全反射は直交偏波、平行偏波ともに存在し、全反射の存在条件はε1<ε2である。
ここでのアニメーションでは磁界の2乗の強さ(エネルギー)を示す。
まだ途中・・・だけど直交偏波のときとほとんど同じ。